Դելտաէդր

Ոչ մեծ խիստ ուռուցիկ դելտաէդրը հանդիսանում է կանոնավոր իկոսաէդր:

Վեցանիստերով (որոնցից յուրաքանչյուրը տրոհված է եռանկյունների) հատած տետրաէդր: Այս մարմինը չի հանդիսանում խիստ ուռուցիկ դելտաէդր, քանի որ մի հարթության մեջ գտնվող նիստերն անթույլատրելի են ըստ սահմանման:

Դելտաէդր, բազմանիստ, որի բոլոր նիստերը հանդիսանում են կանոնավոր եռանկյուններ։ Անվանումը վերցրված է հունական մեծատառ դելտա տառից ($\mathrm{\Delta }$), որն ունի կանոնավոր եռանկյան տեսք։ Գոյություն ունի անթիվ շատ դելտաէդրեր, բայց դրանցից միայն 8-ն են ուռուցիկ, և դրանք ունեն 4, 6, 8, 10, 12, 14, 16 և 20 նիստերԿաղապար:Sfn։

Ութ դելտաէդրերից յուրաքանչյուրի նիստերի, կողերի և գագաթների թիվը թվարկված են ներքևում։

Ուռուցիկ դելտաէդրեր

Գոյություն ունի ընդամենը 8 ուռուցիկ դելտաէդր, որոնցից 3-ը հանդիսանում են պլատոնյան մարմիններ, իսկ 5-ը՝ Ջոնսոնի բազմանիստեր։

6 նիստերով դելտաէդրի որոշ գագաթներ ունեն 3 կարգ, իսկ որոշները՝ 4 կարգ։ 10, 12, 14 և 16 նիստերով դելտաէդրերում որոշ գագաթներ ունեն 4 կարգ, իսկ որոշներն էլ՝ 5 կարգ։ Այդ հինգ ոչ կանոնավոր դելտաէդրերը պատկանում են կանոնավորանիստ բազմանիստերի (որպես նիստ կանոնավոր բազմանկյուններով ուռուցիկ բազմանիստերի) դասին։

Գոյություն չունի 18 նիստերով ուռուցիկ դելտաէդրԿաղապար:Sfn։ Սակայն ձգված կողով իկոսաէդրը տալիս է օկտաէդրի օրինակ, որը կարող է լինել կամ 18 ոչ կանոնավոր նիստերով, կամ երկու զույգ երեքական հավասարակողմ եռանկյուններով՝ ընկած մի հարթության մեջ։

Կանոնավոր դելտաէդրեր
Անվանում	Պատկեր	Գագաթների թիվ	Կողերի թիվ	Նիստերի թիվ	Գագաթի կոնֆիգուրացիա	Սիմետրիայի խումբ
Կանոնավոր տետրաէդր		4	6	4	4 × 33	Td, [3,3]
Կանոնավոր օկտաէդր (քառանկյուն երկբուրգ)		6	12	8	6 × 34	Oh, [4,3]
Կանոնավոր իկոսաէդր		12	30	20	12 × 35	Ih, [5,3]
Ջոնսոնի դելտաէդրեր
Եռանկյուն երկբուրգ		5	9	6	2 × 33 3 × 34	D3h, [3,2]
Հնգանկյուն երկբուրգ		7	15	10	5 × 34 2 × 35	D5h, [5,2]
Հարթաքիթ երկլինոիդ		8	18	12	4 × 34 4 × 35	D2d, [2,2]
Եռակի աճացրած եռանկյուն բուրգ		9	21	14	3 × 34 6 × 35	D3h, [3,2]
Պտտած երկարացրած քառանկյուն երկբուրգ		10	24	16	2 × 34 8 × 35	D4d, [4,2]

Ոչ խիստ ուռուցիկ դեպքեր

Գոյություն ունի կոպլանար եռանկյուններով (միևնույն հարթության մեջ ընկած) անթիվ շատ դելտաէդրեր։ Եթե կոպլանար եռանկյունների բազմությունը հանդիսանում են մի նիստ, կարելի է հաշվել քիչ նիստեր, կողեր և գագաթներ։ Կոպլանար եռանկյուն նիստերը կարող են ձուլվել շեղանկյուն, սեղանակերպ, վեցանկյուն կամ այլ հավասարակողմ բազմանկյուն նիստերի։ Յուրաքանչյուր նիստ պետք է լինի ուռուցիկ պոլիամոնդ, այնպես, ինչպես , , , , , , և , ...

Որոշ ոչ մեծ օրինակներ

Կոպլանար դելտաէդրեր

Պատկեր	Անվանում	Նիստեր	Կողեր	Գագաթներ	Գագաթի կոնֆիգուրացիա	Սիմետրիայի խումբ
	Կցանած օկտաէդր Կցանում. 1 տետրաէդր + 1 օկտաէդր	10	15	7	1 × 33 3 × 34 3 × 35 0 × 36	C3v, [3]
		4 3	12
	Եռանկյուն տրապեցոէդր Կցանում. 2 տետրաէդր + 1 օկտաէդր	12	18	8	2 × 33 0 × 34 6 × 35 0 × 36	C3v, [3]
		6	12
	Կցանում. 2 տետրաէդր + 1 օկտաէդր	12	18	8	2 × 33 1 × 34 4 × 35 1 × 36	C2v, [2]
		2 2 2	11	7
	Եռանկյուն հատած բուրգ Կցանում. 3 տետրաէդր + 1 օկտաէդր	14	21	9	3 × 33 0 × 34 3 × 35 3 × 36	C3v, [3]
		1 3 1	9	6
	Երկարացված օկտաէդր Կցանում. 2 տետրաէդր + 2 օկտաէդր	16	24	10	0 × 33 4 × 34 4 × 35 2 × 36	D2h, [2,2]
		4 4	12	6
	Քառանիստ Կցանում. 4 տետրաէդր + 1 օկտաէդր	16	24	10	4 × 33 0 × 34 0 × 35 6 × 36	Td, [3,3]
		4	6	4
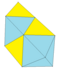
	Կցանում. 3 տետրաէդր + 2 օկտաէդր	18	27	11	1 × 33 2 × 34 5 × 35 3 × 36	D2h, [2,2]
		2 1 2 2	14	9
	Ձգված կողով իկոսաէդր	18	27	11	0 × 33 2 × 34 8 × 35 1 × 36	C2v, [2]
		12 2	22	10
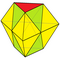
	Երկհատած երկբուրգ Կցանում. 6 տետրաէդր + 2 օկտաէդր	20	30	12	0 × 33 3 × 34 6 × 35 3 × 36	D3h, [3,2]
		2 6	15	9
	Եռաթեք գմբեթ Կցանում. 4 տետրաէդր + 3 օկտաէդր	22	33	13	0 × 33 3 × 34 6 × 35 4 × 36	C3v, [3]
		3 3 1 1	15	9
	Եռանկյուն երկբուրգ Կցանում. 8 տետրաէդր + 2 օկտաէդր	24	36	14	2 × 33 3 × 34 0 × 35 9 × 36	D3h, [3]
		6	9	5
	Վեցանկյուն անտիպրիզմա	24	36	14	0 × 33 0 × 34 12 × 35 2 × 36	D6d, [12,2+]
		12 2	24	12
	Հատած տետրաէդր Կցանում. 6 տետրաէդր + 4 օկտաէդր	28	42	16	0 × 33 0 × 34 12 × 35 4 × 36	Td, [3,3]
		4 4	18	12
	Տետրակիսխորանարդօկտաէդր Օկտաէդր Կցանում. 8 տետրաէդր + 6 օկտաէդր	32	24	18	0 × 33 12 × 34 0 × 35 6 × 36	Oh, [4,3]
		8	12	6

Ոչ ուռուցիկ դելտաէդրեր

Գոյություն ունեն անթիվ շատ ոչ ուռուցիկ և տորոիդալ դելտաէդրեր։

Ինքնահատվող նիստերով դելտաէդրի օրինակ

• Մեծ իկոսաէդր — Կեպլեր - Պուանսոնի մարմին, 20 հատվող եռանկյուններով

  

Ոչ ուռուցիկ այլ դելտաէդրեր կարելի է ստանալ բոլոր հինգ կանոնավոր նիստերին բուրգեր ավելացնելու ճանապարհով.

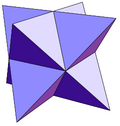
Եռակիստետրաէդր	Տետրակիսհեքսաէդր	Եռակիսօկտաէդր (stella octangula)	Պենտակիսդոդեկաէդր	Եռակիսիկոսաէդր
12 եռանկյուններ	24 եռանկյուններ		60 եռանկյուններ

Տետրաէդրերի այլ կցանումներ.

Օրինակներ. Կցանած տետրաէդրեր

8 եռանկյուններ	10 եռանկյուններ	12 եռանկյուններ

Ինչպես նաև շրջված բուրգերի նիստերի ավելացման եղանակով.

• Ակոսավոր դոդեկաեդր.

Ակոսավոր դոդեկաեդր	Տորոիդալ դելտաէդր
60 եռանկյուններ	48 եռանկյուններ

Գրականություն

• Կաղապար:Ռուսերեն հոդված (Авторы показали, что существует только 8 выпуклых дельтаэдров. )
• Կաղապար:Ռուսերեն հոդված