Ութանիստ

Ութանիստ

Տեսակ	Կանոնավոր բազմանիստ
Նիստ	եռանկյուն
Նիստեր	$8$
Կողեր	$12$
Գագաթներ	$6$
Մի գագաթից ելնող նիստեր	$4$
Գագաթի անկյունը	$2 \arccos \frac{7}{9} \approx 1.3593476$ ստեռ
Կետային համաչափության խումբ	Օկտաեդրական (O_h)
Երկակի բազմանիստ	Խորանարդ

Ութանիստ (Կաղապար:Lang-gr, Կաղապար:Lang-gr, «ութ» и греч. Կաղապար:Lang-gr — «հիմք»), Պլատենյան հինգ հայտնի ուռուցիկ կանոնավոր բազմանիստերից մեկը^[1]։

Բնութագրիչներ

Ութանիստն ունի 8 եռանկյունաձև նիստեր, 12 կող, 6 գագաթ, յուրաքանչյուր գագաթից ելնում են 4 նիստեր։

Եթե ութանիստի կողի երկարությունը а է, ապա լրիվ մակերևույթի մակերեսը (S) և օկտաեդրի ժավալը (V) հաշվվում են հետևյալ բանաձևերով՝

S = 2 a^{2} \sqrt{3}

V = \begin{matrix} \frac{1}{3} \end{matrix} \sqrt{2} a^{3}

Ութանիստին արտագծված գնդի շառավիղը հավասար է՝

r_{u} = \frac{a}{2} \sqrt{2}

,

Ութանիստին ներգծված գնդի շառավիղը հաշվվում է հետևյալ բանաձևով՝

r_{i} = \frac{a}{6} \sqrt{6} .

երկնիստ անկյուն։ $α = 2 ϕ \approx 109, 4 7^{\circ}$ , где $ϕ = a r c c o s (\frac{\sqrt{3}}{3})$ .

Կանոնավոր օկտաէդր

Կանոնավոր օկտաէդրն ունի 8 եռանկյուն նիստ, 12 կող, 6 գագաթ, յուրաքանչյուր գագթից դուրս է գալիս 4 նիստ։

Չափեր

Եթե օկտաէդրի կողի երկարությունը հավասար է а, ապա օկտաէդրին արտագծած գնդային մակերևույթի շառավիղը հավասար է.

r_{u} = \frac{a}{2} \sqrt{2} \approx 0.7071067 \cdot a

,

Օկտաէդրին ներգծյալ գնդային մակերևույթի շառավիղը հաշվում են հետևյալ բանաձևով.

r_{i} = \frac{a}{6} \sqrt{6} \approx 0.4082482 \cdot a :

Երկնիստ անկյունը. $α = 2 ϕ \approx 109, 4 7^{\circ}$ , որտեղ $ϕ = a r c c o s (\frac{\sqrt{3}}{3})$ :

Բոլոր կողերը շոշափող կիսաներգծյալ գնդային մակերևույթի շառավիղը հավասար է

r_{m} = \frac{a}{2} = 0.5 \cdot a

:

Օրթոգոնալ պրոյեկցիաները

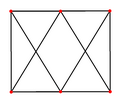
Օկտաէդրն ունի չորս հատուկ օրթոգոնալ պրոյեկցիաներ՝ կենտրոնադրած կողով, գագաթով, նիստով և նիստի նորմալով։ Երկրորդ և երրորդ դեպքը համապատասխանում են Կոքսետերի B₂ և A₂ հարթություններին։

Օրթոգոնալ պրոյեկցիաներ
Կենտրոնադրում	Կողով	Նիստի նորմալով	Գագաթով	Նիստով
Պատկեր
Պրոյեկտիվ համաչափություն	[2]	[2]	[4]	[6]

Գնդային խճանկար

Օկտաէդրը կարելի է ներկայացնել որպես գնդային խճանկար և հարթության վրա պրոյեկտել տարածագրական պրոյեկցիայի օգնությամբ։ Այդ պրոյեկցիան կոնֆորմ է, պահպանում է անկյունները, բայց ոչ երկարություններն ու մակերեսը։ Գնդի վրայի հատվածները հարթության վրա արտապատկերվում են շրջանագծի աղեղների։

Օրթոգոնալ պրոյեկցիա	Տարածագրական պրոյեկցիա
	Եռանկյունա-կենտրոնադրած

Դեկարտյան կոորդինատներ

$\sqrt{2}$ երկարությամբ կողով օկտաէդրը կոորդինատների սկզբնակետից կարող է տեղադրվել այնպես, որ նրա բարձրություններն ընկած լինեն կոորդինատային առանցքների վրա։ Այդ դեպքում գագաթների դեկարտյան կոորդինատները կլինեն.

(±1, 0, 0);

(0, ±1, 0);

(0, 0, ±1):

x-y-z ուղղանկյուն կոորդինատային համակարգում օկտաէդրը դա (a, b, c) կետով կենտրոնով և r շառավղով բոլոր (x, y, z) կետերի բազմությունն է, այնպես, որ

| x - a | + | y - b | + | z - c | = r :

Մակերես և ծավալ

a երկարությամբ կողով կանոնավոր օկտաէդրի լրիվ մակերևույթի մակերեսը հավասար է

S = 2 a^{2} \sqrt{3} \approx 3.46410162 a^{2}

:

Օկտաէդրի ծավալը (V) հաշվարկվում է

V = \begin{matrix} \frac{1}{3} \end{matrix} \sqrt{2} a^{3} \approx 0.471404521 a^{3}

բանաձևով։

Այսպիսով, նույն երկարությամբ կողով օկտաէդրի ծավալը չորս անգամ մեծ է տետրաէդրի ծավալից, իսկ մակերևույթի մակերեսը մեծ է երկու անգամ (քանի որ մակերևույթը կազմված է 8 եռանկյուններից, իսկ տետրաէդրը՝ 4):

Եթե օկտաէդրը ձգենք, որպեսզի տեղի ունենա հետևյալ հավասարությունը.

| \frac{x}{x_{m}} | + | \frac{y}{y_{m}} | + | \frac{z}{z_{m}} | = 1,

մակերեսի և ծավալի բանաձևերը վերածվում են՝

A = 4 x_{m} y_{m} z_{m} \times \sqrt{\frac{1}{x_{m}^{2}} + \frac{1}{y_{m}^{2}} + \frac{1}{z_{m}^{2}}}

V = \frac{4}{3} x_{m} y_{m} z_{m}

Բացի այդ, ձգված օկտաէդրի իներցիայի մոմենտների տենզորը հավասար կլինի.

I = [\begin{matrix} \frac{1}{10} m (y_{m}^{2} + z_{m}^{2}) & 0 & 0 \\ 0 & \frac{1}{10} m (x_{m}^{2} + z_{m}^{2}) & 0 \\ 0 & 0 & \frac{1}{10} m (x_{m}^{2} + y_{m}^{2}) \end{matrix}]

Այն բերվում է կանոնավոր օկտաէդրի հավասարման, երբ. $x_{m} = y_{m} = z_{m} = a \frac{\sqrt{2}}{2}$ :

Երկրաչափական կապեր

Երկու երկակի տետրաէդրերի ներքին (ընդհանուր) փոխդասավորվածության մաս է կազմում օկտաէդրը, իսկ հենց այդ փոխդասավորությունը կոչվում է աստղաձև օկտաէդր (լատ. stella octangula): Փոխդասավորվածությունը հանդիսանում է օկտաէդրի աստղաձև միակ ձևը։ Հետևաբար, կանոնավոր օկտաէդրը հանդիսանում է կանոնավոր տետրաէդրից կողի կեսի երկայնքով չորս կանոնավոր տետրաէդրերով հատույթ։ Օկտաէդրի գագաթները ընկած են տետրաէդրի կողերի մեջտեղում և օկտաէդրը տետրաէդրի հետ կապված է նույն ձևով, ինչպես խորանարդաօկտաէդրը և իկոսոդոեկտաէդրը կապված են պլատոնյան մնացած մարմինների հետ։

Օկտաէդրը պլատոնյան մարմինների շրջանակում յուրահատուկ է նրանով, որ միայն նա յուրաքանչյուր գագաթին կից ունի զույգ թվով նիստեր։

Օկտաէդրը համարվում է 4-կապանի։ Դա նշանակում է, որ պետք է հեռացնել չորս գագաթները, որպեսզի մնացածները հեռացնեն։ Դա 4-կապանի 4 սիմպլիցիալ լավ ծածկույթով բազմանիստերից մեկն է, որը նշանակում է, որ գագաթների ամենաշատ անկախ բազմությունները ունեն նույն չափը։ Այդ հատկություններով մնացած երեք բազմանիստերն են հնգանկյուն երկբուրգը, սիամական դոդեկաէդրը և 12 գագաթներով և 20 եռանկյուն նիստերով անկանոն բազմանիստըԿաղապար:Sfn։

Օկտաէդրը կարելի է ներգծել տետրաէդրին, ընդ որում օկտաէդրի 8 նիստերից 4-ը կլինեն համադրված տետրաէդրի չորս նիստերի հետ, օկտաէդրի բոլոր վեց գագաթները կլինեն համադրված տետրաէդրի վեց կողերի միջնակետերի հետ։
Օկտաէդրը կարելի է ներգծել խորանարդին, ընդ որում օկտաէդրի բոլոր վեց գագաթները համադրված կլինեն խորանարդի վեց նիստերի կենտրոնների հետ։
Օկտաէդրին կարելի է ներգծել խորանարդ, ընդ որում խորանարդի բոլոր ութ գագաթները տեղակայված կլինեն օկտաէդրի ութ նիստերի կենտրոններում։

Համասեռ գունավորում և սիմետրիա

Գոյություն ունի համասեռ գունավորմամբ 5 օկտաէդրեր, անվանված են ըստ իրենց նիստերի գույների. 1212, 1112, 1111:

Օկտաէդրի համաչափության խումբ է հանդիսանում 48 կարգի O_h հիպերօկտաէդրալ եռաչափ խումբը։ Այդ խմբի ենթախմբերի կազմի մեջ է մտնում D_3d (12 կարգի)՝ եռանկյուն անտիպրիզմայի համաչափության խումբը, D_4h (16 կարգի)՝ քառակուսային երկբուրգի համաչափության խումբը և T_d (24 կարգի)՝ ամբողջությամբ հատած տետրաէդրի համաչափության խումբ։ Այդ համաչափությունները կարելի է ընդգծել նիստերի տարատեսակ գունավորման ճանապարհով։

Անվանում	Օկտաէդր	Ամբողջությամբ հատած տետրաէդր (Տետրատետրաէդր)	Եռանկյունային անտիպրիզմա	Քառակուսային երկբուրգ	Շեղանկյունային երկբուրգ
Պատկեր (Նիստերի գունավորում)	(1111)	(1212)	(1112)	(1111)	(1111)
Շլեֆլիի սիմվոլ	{3,4}	r{3,3}	s{2,6} sr{2,3}	ft{2,4} { } + {4}	ftr{2,2} { } + { } + { }
Վիտխոֆֆի սիմվոլ	4 \| 3 2	2 \| 4 3	2 \| 6 2 \| 2 3 2
Համաչափություն	O_h, [4,3], (*432)	T_d, [3,3], (*332)	D_3d, [2⁺,6], (2*3) D₃, [2,3]⁺, (322)	D_4h, [2,4], (*422)	D_2h, [2,2], (*222)
Կարգ	48	24	12 6	16	8

Փռվածքներ

Գոյություն ունի օկտաէդրի 12 փռվածք^[2]։

Երկակիություն

Օկտաէդրը երկակի է խորանարդին։

Հատույթ

Համասեռ տետրահեմիհեկսաէդրը համարվում է կանոնավոր օկտաէդրի տետրաէդրալ համաչափության հետ հատույթ, որը պահպանում է կողերի և գագաթների դասավորությունը։ Հատույթն ունի չորս եռանկյուն նիստեր և 3 կենտրոնական քառակուսի։

Օկտաէդր	Տետրահեմիհեկսաէդր

Ոչ կանոնավոր օկտաէդրեր

Հաջորդ բազմանիստերը կոմբինատոր համարժեք են կանոնավոր օկտաէդրին։ Նրանք բոլորն ունեն վեց գագաթ, ութ եռանկյուն նիստեր և տասներկու կողեր, ինչը համապատասխանում է կանոնավոր օկտաէդրի պարամետրերին։

Եռանկյուն անտիպրիզմաներ՝ երկու նիստերն իրենցից ներկայացնում են զուգահեռ հարթություններում ընկած և համաչափության ընդհանուր առանք ունեցող հավասարակողմ եռանկյուններ։ Մյուս վեց եռանկյունները հավասարակողմ են։
Քառանկյուն երկբուրգեր, որի մեջ ամենաքիչը մեկ էկվատորիալ քառանկյունը ընկած է հարթության մեջ։ Կանոնավոր օկտաէդրը հանդիսանում է հատուկ դեպք, երբ բոլոր երեք քառանկյունները համդիսանում են հարթ քառակուսիներ։
Շոնխարդտի բազմանիստ, ոչ ուռուցիկ բազմանիստ, որն առանց նոր գագաթներ ներմուծելու հնարավոր չէ տրոհել տետրաէդրերի։

Այլ ուռուցիկ ութանիստեր

Ընդհանուր առմամբ, օկտաէդր կարող է անվանվել ութ նիստ ունեցող բազմանիստը։ Կանոնավոր օկտաէդրն ունի 6 գագաթ և 12 կող՝ մինիմալ թիվ օկտաէդրի համար։ Ոչ կանոնավոր ութանիստերը կարող են ունենալ մինչև 12 գագաթ և 18 կող^[2]^[3]։

Գոյություն ունի 257 տոպոլոգիապես տարբեր ուռուցիկ ութանիստեր, հայելային արտապատկերումները բացառած^[2]։ Մասնավորապես, գոյություն ունի 2, 11, 42, 74, 76, 38, 14 ութանիստեր համապատասխանաբար 6-ից մինչև 12 գագաթների թվով^[4]^[5]։

Որոշ ոչ կանոնավոր ութանիստեր.

Ութանկյուն պրիզմա. Երկու նիստերը հանդիսանում են զուգահեռ կանոնավոր վեցանկյուններ, վեց քառակուսիներ զույգ առ զույգ միացնում են վեցանկյունների համապատասխան կողմերը։
Յոթանկյուն բուրգ. Մեկ նիստը հանդիսանում է յոթանկյուն (հիմնականում կանոնավոր), իսկ մնացած յոթ նիստերը հանդիսանում են եռանկյուններ (հիմնականում հավասարասրուն)։ Հնարավոր չէ, որպեսզի բոլոր եռանկյուն նիստերը լինեն հավասարակողմ։
Հատած տետրաէդր. Տետրաէդրի չորս նիստերը հատվում են մինչև կանոնավոր վեցանկյուններ և հատած գագաթների տեղում ձևավորվում են երեք հավելյալ հավասարակողմ եռանկյուն նիստեր ։
Քառանկյուն տրապեցոէդր. Ութ նիստերը կոնգրուենտ են դելտոիդներին։

Օկտաէդրերը ֆիզիկական աշխարհում

Օկտաէդրերը բնության մեջ

Բնական մի շարք խորանարդային բյուրեղներ ունեն օկտաէդրի տեսք։ Դրանք են. ալմաստը, ալյումինակալիումի սուլֆատը, նատրիումի քլորիդը, պերովսկիտը, օլիվինը, ֆլյուորիտը, շպինելը։
Օկտաէդրի ձև ունեն մաքուր մետաղների (նիկել, պղինձ, մագնեզիում, տիտան, լանթան և շատ ուրիշներ) պլատոնափաթեթային կառուցվածքների մեջ միջատոմային դատարկությունները (անցքեր)։
Կամասիտի համաձուլվածքների թիթեղը օկտաէդրիտային երկնաքարերում տեղավորված են ութանիստ օկտաէդրի ութ նիստերին զուգահետ։

Օկտաէդրն արվեստի և մշակույթի մեջ

Խաղերի մեջ օկտաէդրի տեսքի զառը կոչվում է «d8»:
Եթե օկտաէդրի յուրաքանչյուր կող փոխարինենք միաօհմ ռեզիստրով, հանդիպակաց գագաթների միջև դիմադրությունը կկազմի 1/2 Օհմ, իսկ կից գագաթների միջև՝ 5/12 ՕհմԿաղապար:Sfn.
Երաժշտական յոթ նոտաներ օկտաէդրի գագաթների վրա կարելի է դասավորել այնպես, որ յուրաքանչյուր կող ներկայացնի ներդաշնակ զույգ, իսկ յուրաքանչյուր նիստ՝ ներդաշնակ եռյակ։
Հակատանկային ոզնին ունի երեք շեղակի օկտաէդրի ձև։

Տետրաէդալ կապ

Կրկնվող տետրաէդրերից և օկտաէդրերից կազմված կմախքը 1950-ական թվականներին հայտնաբերել է Ֆուլլերը և այն հայտնի է որպես տարածական շրջանակ և համարվում է ամուր կառույց։

Կապված բազմանիստեր

Կանոնավոր օկտաէդր կարելի է ստանալ իրար հաջորդող նիստերի վրա ավելացնելով չորս տետրաէդրեր։ Բոլոր ութ նիստերին տետրադրեր ավելացնելը ձևավորում է աստղաձև օկտաէդր։

Տետրաէդր	Աստղաձև օկտաէդր

Տետրատետրաէդր

Կանոնավոր օկտաէդրը կարելի է դիտարկել որպես ամբողջական հատած տետրաէդր և կարող է անվանվել տետրատետրաէդր։ Դա կարելի է ցույց տալ երկու գույնով ներկված մոդելով։ Այդ գունավորմամբ օկտաէդրն ունենում է տետրաէդրալ համաչափություն։

Համասեռ տետրաէդրալ բազմանիստերի ընտանիք
Համաչափություն։ [3,3], (*332)							[3,3]⁺, (332)

{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
Երկակի բազմանիստեր

V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

Օկտաեդրի հատկությունները

Օկտաեդրին կարելի է ներգծել տետրաեդր, ընդ որում ութանիստի ութ նիստերից չորսը ընկած են տետրաեդրի չորս նիստերի հարթությունների վրա, օկտաեդրի բոլոր վեց գագաթները համընկնում են տետրաեդրի վեց կողերի միջնակետերին հետ։
Օկտաեդրը կարելի է ներգծել խորանարդին, ընդ որում ութանիստի բոլոր վեց գագաթները ընկած կլինեն խորանարդի նիստերի կենտրոնների վրա։
Օկտաեդրին կարելի է ներգծել խորանարդ, ընդ որում խորանարդի բոլոր ութ գագաթները կհամընկնեն օկտաեդրի ութ նիստերի կենտրոնների հետ։
Կանոնավոր ութանիստը ունի համաչափության O_h կենտրոն, որը համընկնում է խորանարդի կենտրոնի հետ։

Ութանկյունը բնության մեջ

Բնության մեջ հանդիպող շատ բյուրեղներ ունեն հենց օկտաեդրի տեսք։ Օրինակ, ալմաստը, նատրիումի քլորիդը, պերովսկիտը, օլիվինը, ֆլյուորիտը, շպինելը։

Ալմաստ
Նատրիումի քլորիդ
Պերովսկիտ
Օլիվին
Ֆլյուորիտ
Շպինել

Ութանիստի տեսք ունեն միջատոմային հեռավորությունները կիպ փաթեթվոչված մաքուր մետաղներում (նիկելի, պղնձի, մագնեզիումի, տիտանի, լանթանի և այլ մետաղների) ու իոնական միացություններում (նատրիումի քլորիդ, սֆալերիտ, վյուրցիտ և այլն)։

Տես նաև

Կոմպլեքս միացություններ

Ծանոթագրություններ

Կաղապար:Ծանցանկ

Գրականություն

Կաղապար:Refbegin

Կաղապար:Refend

Արտաքին հղումներ

Կաղապար:ՀՍՀ

↑ Սելիվանով Դ. Ֆ., Երկրաչափական մարմին։ Բրոքհաուսի ու Եֆրոնի հանրագիտարանային բառարան 86 հատորով (82-րդ հատոր և 4 լրացուցիչ) 1890 —1907
↑ ^2,0 ^2,1 ^2,2 Կաղապար:MathWorld3
↑ Կաղապար:Cite web
↑ Counting polyhedra
↑ Կաղապար:Cite web

[1] Սելիվանով Դ. Ֆ., Երկրաչափական մարմին։ Բրոքհաուսի ու Եֆրոնի հանրագիտարանային բառարան 86 հատորով (82-րդ հատոր և 4 լրացուցիչ) 1890 —1907

[mw-2] 2,0 ^2,1 ^2,2 Կաղապար:MathWorld3

[3] Կաղապար:Cite web

[4] Counting polyhedra

[5] Կաղապար:Cite web

[1]

[2]

[3]

[4]

[5]

Ութանիստ

Բովանդակություն

Բնութագրիչներ