Սեղան (երկրաչափություն)

Կաղապար:Անաղբյուր Կաղապար:Այլ կիրառումներ

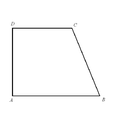
Սեղան է կոչվում այն քառանկյունը, որի երկու հանդիպակաց կողմերը զուգահեռ են միմյանց, իսկ մյուս երկուսը՝ ոչ։

Սեղանի զուգահեռ կողմերը կոչվում են հիմքեր։ (Օրինակ՝ նկարում AB-ն սեղանի փոքր հիմքն է, DC-ն՝ մեծ հիմքը)

Սեղանի ոչ զուգահեռ կողմերը կոչվում են սրունքներ։ (Օրինակ՝ նկարում AD-ն, BC-ն)

Սեղանները կարող են լինել հավասարասրուն և ուղղանկյուն։ Հավասարասրուն սեղան է կոչվում այն սեղանը, որի սրունքները (կողմնային կողերը) հավասար են միմյանց։ Իսկ ուղղանկյուն սեղան է կոչվում այն սեղանը, որի սրունքներից մեկը ուղղահայաց է հիմքերին^[1]։

Սեղանի տարրերի սահմանումներ

Սեղանի տարրեր

Զուգահեռ կողմերը կոչվում են հիմքեր․
2 մյուս կողմերը կոչվում են սրունքներ.
Սրունքների միջնակետերը միացնող գիծը կոչվում է սեղանի միջին գիծ.

Սեղանների տեսակներ

Այն սեղանները, որոնց սրունքները հավասար են կոչվում են հավասարասրուն սեղաններ^[2]։
Այն սեղանը, որն ունի ուղիղ անկյուն, կոչվում է ուղղանկյուն սեղան։

Հավասարասրուն սեղան
Ուղղանկյուն սեղան

Ընդհանուր հատկություններ

Սեղանի բարձրությունը

h = \sqrt{c^{2} - \frac{1}{4} {(\frac{c^{2} - d^{2}}{b - a} + b - a)}^{2}}

որտեղ

b

— մեծ հիմքն է,

a

— փոքր հիմքն է,

c

и

d

— սրունքներ.

$d_{1}$ և $d_{2}$ անկյունագծերը, և կողմերը կապված են

d_{1}^{2} + d_{2}^{2} = 2 a b + c^{2} + d^{2}

արտահայտությամբ։

Անկյունագծերը արտահայտվում են՝

d_{1} = A C = \sqrt{a b + d^{2} + \frac{b (c^{2} - d^{2})}{b - a}}

d_{2} = B D = \sqrt{a b + c^{2} - \frac{b (c^{2} - d^{2})}{b - a}}

Եվ ընդհակառակը՝

a = \sqrt{\frac{(c^{2} - d_{1}^{2})^{2} - (d^{2} - d_{2}^{2})^{2}}{2 (c^{2} - d^{2} + d_{1}^{2} - d_{2}^{2})}}

b = \sqrt{\frac{(c^{2} - d_{2}^{2})^{2} - (d^{2} - d_{1}^{2})^{2}}{2 (c^{2} - d^{2} - d_{1}^{2} + d_{2}^{2})}}

c = \sqrt{\frac{a (d_{2}^{2} - b^{2}) + b (d_{1}^{2} - a^{2})}{a + b}}

d = \sqrt{\frac{a (d_{1}^{2} - b^{2}) + b (d_{2}^{2} - a^{2})}{a + b}}

Եթե հայտնի է

h

բարձրությունը,ապա

d_{1} = \sqrt{b^{2} + d^{2} - 2 b \sqrt{d^{2} - h^{2}}} = \sqrt{h^{2} + {(b - \sqrt{d^{2} - h^{2}})}^{2}}

d_{2} = \sqrt{b^{2} + c^{2} - 2 b \sqrt{c^{2} - h^{2}}} = \sqrt{h^{2} + {(b - \sqrt{c^{2} - h^{2}})}^{2}}

Ներգծված և արտագծված շրջանագծեր

Արտագծված շրջանագծի շառավիղը՝

R = \frac{b c d_{1}}{4 \sqrt{p (p - b) (p - c) (p - d_{1})}} = \sqrt{\frac{a b + c^{2}}{4 - {(\frac{b - a}{c})}^{2}}}

որտեղ

p = \frac{1}{2} (b + c + d_{1}), c

— սրունք,

b

— մեծ հիմք,

a

— փոքր հիմք,

d_{1} = d_{2}

— հավասարասրուն սեղանի անկյունագծերը

Եթե $a + b = 2 c$ , ապա հավասարասրուն սեղանին կարելի է ներգծել,

r = \frac{h}{2} = \frac{\sqrt{a b}}{2}

շառավղով շրջանագիծ։

Սեղանի մակերեսը

$a$ և $b$ սեղանի հիմքերի և $h$ — բարձրության միջոցով՝

S = \frac{(a + b)}{2} h

$m$ միջին գծի և $h$ բարձրության միջոցով՝

S = m h

միջին գիծը հավասար է հիմքերի կիսագումարին՝

m = \frac{(a + b)}{2}

սեղանի մակերեսը $a$ , $b$ հիմքերի և $c$ և $d$ ոչ զուգահեռ կողմերի միջոցով՝

S = \frac{a + b}{4 | a - b |} \sqrt{(a + c + d - b) (a + d - b - c) (a + c - b - d) (b + c + d - a)} .

հավասարասրուն սեղանի մակերեսը $r$ ներգծված շրջանագծի շառավիղի և հիմքին կից $α$ անկյան միջոցով՝

S = \frac{4 r^{2}}{\sin α}

մասնավորապես, եթե տվյալ անկյունը 30° է, ապա

S = 8 r^{2}

հավասարասրուն սեղանի մակերեսը $c$ կողմի և $a$ մեծ հիմքին կից $γ$ անկյան միջացով։

S = (a - c \cos γ) c \sin γ = (b + c \cos γ) c \sin γ

Ծանոթագրություններ

Կաղապար:Ծանցանկ

[1] Trapezoid - from Wolfram MathWorld

[2] Հավասարասրուն սեղան - իմդպրոց․ամ

[1]

[2]

Սեղան (երկրաչափություն)

Բովանդակություն

Սեղանի տարրերի սահմանումներ

Սեղանի տարրեր

Սեղանների տեսակներ

Ընդհանուր հատկություններ

Ներգծված և արտագծված շրջանագծեր

Սեղանի մակերեսը

Ծանոթագրություններ

Նավարկման ցանկ

Սեղան (երկրաչափություն)

Սեղանի տարրերի սահմանումներ

Սեղանի տարրեր

Սեղանների տեսակներ

Ընդհանուր հատկություններ

Ներգծված և արտագծված շրջանագծեր

Սեղանի մակերեսը

Ծանոթագրություններ

Նավարկման ցանկ

Որոնում