Քառանկյուն

Քառանկյուն
┌─────────────┼────────────┐
Ոչ ուռուցիկ		Ուռուցիկ		Ինքնահատվող
┌─────────────┼─────────────┐
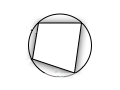
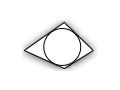
Շրջանագծով արտագծված		Սեղան		Շրջանագծով ներգծված
| ┌───────────┤				|
Հավասարասրուն սեղան Սրունքները հավասար են		Զուգահեռագիծ 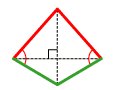Կողմերը զուգահեռ են		Դելտոիդ Անկյունագծերն ուղղահայաց են
└─────┬─────┘			└─────┬─────┘
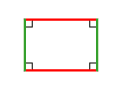Ուղղանկյուն Ուղիղ անկյուններ			Շեղանկյուն Հավասարասրուն
└──────────┬─────────┘
Քառակուսի

Քառանկյուն, երկրաչափական պատկեր, որը կազմված է 4 գագաթից (դրանցից 3-ը մեկ ուղղի վրա ընկած չեն) և 4 ուղղից, որոնք միացնում են գագաթները։ Տարբերում են ուռուցիկ և ոչ ուռուցիկ քառանկյուններ։

Քառանկյան տեսակները

• Զուգահեռագիծ՝ քառանկյուն, որի հանդիպակած կողմերը զույգ առ զույգ զուգահեռ են և հավասար
• Ուղղանկյուն՝ քառանկյուն, որի բոլոր անկյուններն ուղիղ են
• Շեղանկյուն՝ քառանկյուն, որի բոլոր կողմերը հավասար են
• Քառակուսի՝ քառանկյուն, որի բոլոր անկյունները ուղիղ են, իսկ բոլոր կողմերը՝ հավասար
• Սեղան՝ քառանկյուն, որի երկու հակադիր կողմերը զուգահեռ են
• Դելտոիդ՝ քառանկյուն, որի իրար կապված երկու կողմերի երկու զույգ հավասար են

Քառանիստ

Չնայած այս անվանումը կարող է համարժեք չլինել քառանկյան հետ, բայց նրան հաճախ տրվում է հավելյալ իմաստ։ Քառանկյուն է կոչվում այն 4 գծերը, որոնցից ցանկացած երկուսը զուգահեռ չեն և ցանկացած երեքը չեն անցնում մեկ կետով։

Հիմնական տեղեկություններ

• Քառանկյան անկյունների գումարը հավասար է 2π = 360°։
• Քառանկյանը կարելի է արտագծել շրջանագիծ այն և միայն այն դեպքում, երբ հակադիր անկյունների գումարը հավասար է 180°՝

($\mathrm{\angle }A+\mathrm{\angle }C=\mathrm{\angle }B+\mathrm{\angle }D=180^{\circ }$)

• Ուռուցիկ քառանկյունը հանդիսանում է ներգծված շրջանագծով այն և միայն այն դեպքում, երբ հակադիր կողմերի երկարությունները հավասար են ($AB+CD=BC+AD$)։
• Էյլերի բանաձևը. Տրամագծերի հատույթի տարածության քառակուսու քառապատիկը հավասար է քառանկյան կողմերի քառակուսու և իր տրամագծերի քառակուսու տարբերությանը։
• Քառանկյան միջին գիծը և քառանկյան տրամագծերի հատույթը միացնող հատվածը հատվում են և կիսվում։
• Չորս հատվածները, որոնցից յուրաքանչյուրը քառանկյան գագաթը միացնում է մյուս 3 գագաթներից կազմված եռանկյան կենտրոնին, հատվում են քառանկյան կենտրոնում և բաժանվում 3։1 հարաբերությամբ հատվածների՝ հաշված գագաթից։
• Քառանկյան երկու հանդիպակաց կողմեր ուղղահայաց են այն և միայն այն դեպքում, երբ մյուս երկու կողմերի քառակուսիների գումարը հավասար է անկյունագծերի քառակուսիների գումարին։
• Քառանկյան անկյունագծերը ուղղահայաց են այն և միայն այն դեպքում, որբ հակադիր կողմերի քառակուսիների գումարները հավասար են։
• 4 կամայական կետերի միջև ընկած 6 հեռավորությունները, որոնք վերցված են զույգ առ զույգ, կապված են հետևյալ հարաբերակցությամբ՝

$a^2{c}^2(b^2+d^2+e^2+f^2-a^2-c^2)+b^2{d}^2(a^2+c^2+e^2+f^2-b^2-d^2)+$

$+e^2{f}^2(a^2+c^2+b^2+d^2-e^2-f^2)=(abe{)}^2+(bcf{)}^2+(cde{)}^2+(daf{)}^2$.

Այս հավասարումը կարելի է ներկայացնել հետևյալ տեսքով՝

$\left|\begin{array}{ccccc}0& a^2& e^2& d^2& 1\\ a^2& 0& b^2& f^2& 1\\ e^2& b^2& 0& c^2& 1\\ d^2& f^2& c^2& 0& 1\\ 1& 1& 1& 1& 0\end{array}\right|=0$

Մակերես

$d_1$, $d_2$ անկյունագծեր և նրանց միջև ընկած $\alpha$ անկյուն ունեցող ուռուցիկ քառանկյան մակերեսը հավասար է

$S=\frac{d_1{d}_2\sin \alpha }{2}$

Կամայական քառանկյան մակերեսը հավասար է

• $16S^2=4d_1^2{d}_2^2-{(b^2+d^2-a^2-c^2)}^2$, որտեղ $d_1$, $d_2$ — անկյունագծեր, իսկ a, b, c, d —ն կողմերի երկարություններն են։
• $S=\sqrt{(p-a)(p-b)(p-c)(p-d)-abcd{\cos }^2\theta },$, որտեղ p-ն կիսապարագիծն է, իսկ $\theta$-ն՝ քառանկյան հակառակ կողմերի կիսագումարը (կապ չունի, թե որ զույգն է վերցված, քանի որ եթե մի համադիր զույգի կիսագումարը հավասար է $\theta$, ապա մյուս անկյունների կիսագումարը հավասար կլինի $180^{\circ }-\theta$ և ${\cos }^2(180^{\circ }-\theta )={\cos }^2\theta$)։

Բացառություններ

Եթե քառանկյունը և՛ ներգծված է, և՛ արտագծված, ապա $S=\sqrt{abcd}$։ Եթե այն արտագծված է, ապա մակերեսը հավասար է նրա պարագծի և ներգծված շրջանագծի շառավղի արտադրյալին։

Պատմություն

Հին Եգիպտոսում մի քանի այլ ազգեր մակերեսը հաշվելու համար օգտագործում էին ոչ ճիշտ բանաձև՝

$S=\frac{a+c}{2}\cdot \frac{b+d}{2}$։

Տես նաև

• Կոսինուսների թեորեմ