Միխաելիս-Մենթենի հավասարում

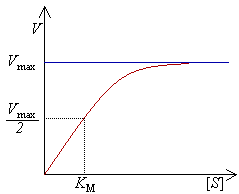
Ռեակցիայի արագության (V) կախվածությունը սուբստրատի կոնցենտրացիայից ([S]) արտահայտող գրաֆիկ

Միխաելիս-Մենթենի հավասարում, կենսաքիմիայում ֆերմենտատիվ ռեակցիաների կինետիկայի հիմնարար հավասարում։ Այն անվանվել է գերմանացի կենսաքիմիկոս Լեոնոր Միխաելիսի և կանադացի ֆիզիկոս Մոդ Մենթենի պատվին։ Այս հավասարումը իրենից ներկայացնում է ֆերմենտատիվ ռեակցիայի $v$ արագության կախվածությունը ռեակցիայի ելանյութի՝ սուբստրարի $[S]$ կոնցենտրացիայից։ Հիմնարար հավասարումը գրվում է հետևյալ կերպով

v = \frac{d [P]}{d t} = \frac{V_{\max} [S]}{K_{m} + [S]}

որտեղ՝

$V_{\max}$ - համակարգի հնարավոր առավելագույն արագություն,
$K_{m}$ - Միխաելիսի հաստատուն, սուբստրատրի այն կոնցենտրացիան, որի դեպքում $V = V_{\max} / 2$ ^[1]։

Ընդունված է համարել, որ մեկ սուբստրատ պարունակով կենսաքիմիական ռեակցիաները ընթանում են Միխաելիս-Մենթենի առաջարկած մեխանիզմով։

Նախատիպ

1903 թվականին ֆրանսիացի ֆիզիկական քիմիկոս Վիկտոր Անրին հայտնաբերել է, որ ֆերմենտատիվ ռեակցիաները ուղեկցվում են ֆերմենտի և սուբստրարի միջև հատուկ կապերի առաջացմամբ^[2]։ Նրա աշխատանքը հետագայում ուսումնասիրվել է գերմանացի կենսաքիմիկոս Լեոնոր Միխաելիսի և կանադացի ֆիզիկոս Մոդ Մենթենի կողմից, ովքեր հիմք են դրել ֆերմենտատիվ ռեակցիաների կինետիկային և առաջին անգամ հայտնաբերել են ինվերտազա ֆերմենտի ազդման մեխանիզմը, որով նա կատալիզում է սախարոզի հիդրոլիզը մինչև գլյուկոզ և ֆրուկտոզ^[3]։ 1913 թվականին նրանք առաջարկեցին այս ռեակցիայի մաթեմատիկական մոդելը, որը հետագայում ընդլայնվեց և հիմք հանդիսացավ քիմիայի նոր բնագավառի զարգացմանը^[4]։ Մեխանիզմն իր մեջ է ներառում $E$ էնզիմի կապումը $S$ սուբստրատի հետ, որի հետևանքով նախ առաջանում է էնզիմ-սուբստրատային $E S$ կոմպլեքսը, որը հետագայում վերածվում է $P$ պրոդուկտի և $E$ էնզիմի։ Սխեմատիկորեն այս մեխանիզմը կարելի է պատկերել հետևյալ կերպով

E + S \overset{k_{f}}{⇌ k_{r}} E S \overset{k_{c a t}}{⟶} E + P

,

որտեղ $k_{f}$ , $k_{r}$ և $k_{c a t}$ իրենցից ներկայացնում են համապատասխան ռեակցիաների արագության հաստատունները^[5], իսկ $S$ -ի և $E S$ -ի միջև կրկնակի սլաքը ցույց է տալիս, որ էնզիմի կապումը սուբստրատին դարձելի ռեակցիա է։

Որոշ մոտավորություններ անելուց հետո կարելի է ասել, որ պրոդուկտի առաջացման արագությունը տրվում է հետևյալ բանաձևով

v = \frac{d [P]}{d t} = V_{\max} \frac{[S]}{K_{m} + [S]} = k_{c a t} [E]_{0} \frac{[S]}{K_{m} + [S]}

Ռեակցիայի արագությունը մեծանում և ձգտում է առավելագույն $V_{\max}$ արժեքին (այն արագությունը, որի դեպքում ամբողջ էնզիմը կապվել է սուբստրատի հետ), երբ մեծանում է սուբստրատի կոնցենտրացիան ( $[S]$ )։ Ցույց է տրված նաև, որ $V_{\max} = k_{c a t} [E]_{0}$ , որտեղ $[E]_{0}$ - ֆերմենտի կոնցենտրացիան է, իսկ $k_{c a t}$ - սուբստրատի մոլեկուլների այն առավելագույն քանակը, որը վերածվել է պրոդուկտի միավոր ժամանակում և մեկ էնզիմի վրա հաշվարկած։

Միխաելիսի $K_{m}$ հաստատունը իրենից ներկայացնում է սուբստրատրի այն կոնցենտրացիան, որի դեպքում $V = V_{\max} / 2$ ^[1], բացի այդ, այն բնութագրում է սուբստրատի հակաաֆինությունը էնզիմի նկատմամբ (որքան փոքր է $K_{m}$ -ը, այնքան մեծ է աֆինությունը, հետևաբար արագությունը ավելի արագ կհասնի $V_{\max}$ -ին^[6])։ $K_{m}$ -ի արժեքը կախված է ինչպես էնզիմից և սուբստրատից, այնպես էլ ռեակցիայի կատարման պայմաններից (ջերմաստիճան, pH)։

Այս նախատիպը օգտագործվում է նաև բազմաթիվ այլ կենսաքիմիական ոլորտներում (հակածին-հակամարմին փոխազդեցություն, ԴՆԹ-ԴՆԹ հիբրիդացում, սպիտակուց-սպիտակուց փոխազդեցություն^[6]^[7])։ Այն կարող է կիրառվել նաև ընդհանուր կենսաքիմիական ռեակցիաներ ուսումնասիրելիս, օրինակ՝ Լենգմյուրի հավասարման փոխարեն, որը թույլ է տալիս կազմել կենսաբանական օբյեկտների ադսորբցիայի մոդել կամ Մոնոդի հավասարման փոխարեն, որը թույլ է տալիս գնահատել մանրէի աճը^[7]։

Միխաելիս-Մենթենի հավասարումը կիրառվում է ոչ միայն կենսաքիմիայում, այլ նաև բազմաթիվ այլ բնագավառներում (փոշու հատիկի ալվեոլային մաքրության որոշում^[8], ջրավազանների կենդանական աշխարհի առատության որոշում^[9], արյան մեջ ալկոհոլի քանակության որոշում^[10], ֆոտոսինթեզ-ճառագայթում կախվածության որոշում^[11], բակտերիալ վարակների ուսումնասիրություն^[12])։

Կիրառություն

Ֆերմենտների պարամետրերը խստիվ տարբերվում են մեկը մյուսից^[13]։

Ֆերմենտ	$K_{m}$ (Մ)	$k_{cat}$ (1/վ)	$k_{cat} / K_{m}$ (1/Մ $\cdot$ վ)
Խիմոտրիպսին	1.5 × 10⁻²	0.14	9.3
Պեպսին	3.0 × 10⁻⁴	0.50	1.7 × 10³
Թիրոզիլ-փՌՆԹ սինթետազ	9.0 × 10⁻⁴	7.6	8.4 × 10³
Ռիբոնուկլեազներ	7.9 × 10⁻³	7.9 × 10²	1.0 × 10⁵
Կարբոնատ դեհիդրազ	2.6 × 10⁻²	4.0 × 10⁵	1.5 × 10⁷
Ֆումարազ	5.0 × 10⁻⁶	8.0 × 10²	1.6 × 10⁸

$k_{cat} / K_{m}$ հաստատունը ցույց է տալիս, թե որքան է ֆերմենտի արդյունավետությունը սուբստրատին պրոդուկտ դարձնելու գործում։ Այն ունի մոտավոր վերին սահման (Կաղապար:Nowrap)։ Այն ֆերմենտները, որոնք աշխատում են այդ տիրույթում (ֆումարազա), կոչվում են գերարդյունավետ^[14]։

Կինետիկական բնութագիր

Դիտարկենք Միխաելիս-Մենթենի առաջարկած մեխանիզմը

E + S \overset{k_{f}}{⇌ k_{r}} E S \overset{k_{c a t}}{⟶} E + P

Կիրառելով զանգվածների ներգործության օրենքը, որը պնդում է, որ ռեակցիայի արագությունը ուղիղ համեմատական է ելանյութերի կոնցենտրացիաների արտադրյալին, ստանում ենք չորս ոչ գծային դիֆերենցիալ հավասարումներ^[15]։

\begin{matrix} \frac{d [E]}{d t} & = - k_{f} [E] [S] + k_{r} [E S] + k_{c a t} [E S] \\ \frac{d [S]}{d t} & = - k_{f} [E] [S] + k_{r} [E S] \\ \frac{d [E S]}{d t} & = k_{f} [E] [S] - k_{r} [E S] - k_{c a t} [E S] \\ \frac{d [P]}{d t} & = k_{c a t} [E S] . \end{matrix}

Այս մեխանիզմում $E$ էնզիմը հանդիսանում է կատալիզատոր, որը միայն արագացնում է ռեակցիան, միաժամանակ նրա ամբողջ կոնցենտրացիան (կապված և ազատ ձևերի կոնցենտրացիաների գումարը՝ $[E] + [E S] = [E]_{0}$ ) հաստատուն մեծություն է։ Այս հավասարությունը հնարավոր է ստանալ նաև գումարելով առաջին և երրորդ դիֆերենցիալ հավասարումները^[15]^[16]։

Հավասարակշռային մոտավորություն

Իրականում Միխաելիսը և Մենթենը համարել են, որ սուբստրատը անմիջապես հավասարակշռության մեջ է մտնում կոմպլեքսի հետ և $k_{f} [E] [S] = k_{r} [E S]$ ^[4]^[16]։ Կիրառելով այս արտահայտությունը էնզիմի պահպանման օրենքի հետ համատեղ, ստանում ենք, որ կոմպլեքսի կոնցենտրացիան հավասար է^[16]

[E S] = \frac{[E]_{0} [S]}{K_{d} + [S]}

,

որտեղ $K_{d} = k_{r} / k_{f}$ իրենից ներկայացնում է էնզիմ-սուբստրատային կոմպլեքսի դիսոցման հաստատունը։

Հետևաբար ռեակցիայի $v$ արագությունը ( $P$ պրոդուկտի առաջացման արագությունը) հավասար է^[16]

v = \frac{d [P]}{d t} = \frac{V_{\max} [S]}{K_{d} + [S]}

,

որտեղ $V_{\max} = k_{c a t} [E]_{0}$ - ռեակցիայի առավելագույն արագությունն է։

Քվազիստացիոնար մոտավորություն

1925 թվականին բրիտանացի բուսաբան Ջորջ Էդվարդ Բրիգսը և բրիտանացի գենետիկ Հոլդեյնը առաջարկեցին այս մեխանիզմի մեկ այլ կինետիկական մեկնաբանություն^[17]։ Նրանք համարեցին, որ միջանկյալ կոմպլեքսի (ինտերմեդիատի) կոնցենտրացիան չի փոխվում պրոդուկտի առաջացման ժամանակից կախված (քվազիստացիոնար մոտավորություն)։ Մաթեմատիկորեն այս մոտավորությունը կարելի է գրել հետևյալ կերպով

$k_{f} [E] [S] = k_{r} [E S] + k_{c a t} [E S]$

Կիրառելով այս արտահայտությունը էնզիմի պահպանման օրենքի հետ համատեղ, ստանում ենք, որ կոմպլեքսի կոնցենտրացիան հավասար է^[16]

[E S] = \frac{[E]_{0} [S]}{K_{m} + [S]}

,

որտեղ $K_{m} = \frac{k_{r} + k_{c a t}}{k_{f}}$ և հայտնի է Միխաելիսի հաստատուն անվանմամբ,

և որտեղ $k_{r}$ , $k_{c a t}$ և $k_{f}$ համապատասխան ռեակցիաների արագության հաստատուններն են։

Հետևաբար ռեակցիայի $v$ արագությունը ( $P$ պրոդուկտի առաջացման արագությունը) հավասար է^[16]

v = \frac{d [P]}{d t} = \frac{V_{\max} [S]}{K_{m} + [S]}

Մոտավորություններ և սահմանափակումներ

Առաջին մոտավորությունը կայանում է զանգվածների ներգործության օրենքի կիրառումը, քանի որ այն պահանջում է ազատ դիֆուզիա։ Պարզ է, որ կենդանի օրգանիզմի բջջում, որտեղ կա սպիտակուցների մեծ կոնցենտրացիա և, բացի այդ, ցիտոպլազման իրենից ներկայացնում է ավելի շուտ դոնդողանման, քան հեղուկ միջավայր, ապա մոլեկուլների շարժումները այդ միջավայրում խիստ սահմանափակված են^[18]։ Քանի դեռ զանգվածների ներգործության օրենքը թույլ է տալիս այն կիրառել հետերոգեն համակարգերում^[19], ապա նպատակահարմար կլինի ցիտոպլազման դիտել որպես ֆրակտալ^[20]։

Երկու տարբեր մոտավորություններով ստացված ռեակցիայի արագությունները գրեթե նույնն են։ Տարբերությունը կայանում է նրանում, որ հավասարակշռային մոտավորությունը բերում է $K_{d}$ հաստատունին, իսկ քվազիստացիոնար մոտավորությունը՝ $K_{m}$ հաստատունին։ Միխաելիս-Մենթենի հավասարակշռային մոտավորությունը ճիշտ է կիրառել այն դեպքում, երբ սուբստրատը հասնում է հավասարակշիռ վիճակի ավելի շուտ, քան առաջանում է պրոդուկտը կամ ավելի ճիշտ^[16], երբ

ϵ_{d} = \frac{k_{c a t}}{k_{r}} ≪ 1

Բրիգս-Հոլդեյնի քվազիստացիոնար մոտավորությունը ճիշտ է կիրառել^[15]^[21], երբ

ϵ_{m} = \frac{[E]_{0}}{[S]_{0} + K_{m}} ≪ 1

Այսինքն այս մոտավորությունը տեղի ունի, եթե ֆերմենտի կոնցենտրացիան շատ փոքր է սուբստրատի կոնցենտրացիայից։ Եթե այս պահանջը բավարարված չէ, ապա $K_{m}$ հաստատունի մեծ արժեքները նույնպես ընդունելի պայման են հանդիսանում։

Ե՛վ Միխաելիս-Մենթենի, և՛ Բրիգս-Հոլդեյնի կատարած մոտավորությունները ավելի լավ տեսք են ընդունում, երբ $ϵ$ -ը նվազում է^[16]։

Շատ կարևոր պայման է նաև այն հանգամանքը, որ պետք է հաշվի առնել, որ ոչ մի ռեակցիա չի ընթանում մեկ ուղղությամբ։ Հետևաբար ֆերմենտատիվ ռեակցիայի մեխանիզմը ճիշտ կլինի գրել հետևյալ տեսքով

E + S \overset{k_{f_{1}}}{\underset{k_{r_{1}}}{⇌}} E S \overset{k_{f_{2}}}{\underset{k_{r_{2}}}{⇌}} E + P

Իրականում, կարելի է համարել, որ ռեակցիան անդարձելի է, եթե պահպանվում է հետևյալ պայմաններից գոնե մեկը
1. Սուբստրատ(ներ) ի կոնցենտրացիան շատ մեծ է պրոդուկտ(ներ) ի կոնցենտրացիայից

[S] ≫ [P]

Այս պայմանը ճիշտ է հատուկ in vitro և բազմաթիվ in vivo պայմաններում ընթացող կենսաբանական ռեակցիաների համար։
2. Ռեակցիայից անջատված էներգիան շատ մեծ է

Δ G ≪ 0

Այն դեպքերում, երբ տեղի չունի հետևյալ երկու պայմաններից և ոչ մեկը, ապա սխալ է օգտագործել Միխաելիս-Մենթենի մոդելը։ Դրա փոխարեն կիրառում են ավելի բարդ մոդելավորման օրինակներ։

Հաստատունների որոշում

$V_{\max}$ և $K_{m}$ հաստատունների որոշման համար դիտարկում են նույն ֆերմենտատիվ ռեակցիան սուբստրատի տարբեր սկզբնական կոնցենտրացիաների համար և սկզբից չափում են ֆերմենտատիվ ռեակցիայի սկզբնական $v_{0}$ արագությունը։ Սկզբնական ասելով նկատի ունեն, որ ռեակցիայի արագությունը չափվել է այն կարճ ժամանակում, երբ էնզիմ-սուբստրատային կոմպլեքս է գոյացել, և, բացի այդ, սուբստրատի կոնցենտրացիան մնացել է մոտավորապես հաստատուն^[21]։ Ապա այդ հաստատունները կարելի է ստանալ կառուցելով ռեակցիայի արագության կախումը կոնցենտրացիայից արտահայտող գրաֆիկը^[22]։

Նախքան համակարգչային մոդելավորման ի հայտ գալը կիրառվել են բազմաթիվ այլ հավասարումներ այդ հաստատունների որոշման համար (Էդի-Հոֆսթիի դիագրամ, Հան-Վուլֆի դիագրամ^[22], Լայնովեր-Բերգի դիագրամ)։

1997 թվականին Սանտյագո Շնելը և Կլաուդիո Մենդոզան առաջարկեցին Միխաելիս-Մենթենի մեխանիզմի լուծման փակ մի եղանակ^[23]։ Այժմ այն կրում է Շնել-Մենդոզայի հավասարում անվանումը և ունի հետևյալ տեսքը

\frac{[S]}{K_{M}} = W [F (t)]

,

որտեղ W[]՝ Լամբերտի W-ֆունկցիան է, իսկ F (t)-ն իրենից ներկայացնում է հետևյալ ֆունկցիան

F (t) = \frac{[S]_{0}}{K_{M}} \exp (\frac{[S]_{0}}{K_{M}} - \frac{V_{\max}}{K_{M}} t)

Շնել-Մենդոզայի հավասարումը ներկայումս լայնորեն կիրառվում է ֆերմենտատիվ ռեակցիաների $V_{\max}$ և $K_{m}$ հաստատունների որոշման համար^[24]^[25]։

Ստորև տրված հավասարումը առաջարկվել է 2010 թվականին Մարիո Բարբերան-Սանթոսի կողմից և այն ևս լավ մոդել է ծառայում ռեակցիայի հաստատունների որոշման համար^[26]։

\frac{[S]}{K_{M}} = W [F (t)] - \frac{V_{\max}}{k_{c a t} K_{M}} \frac{W [F (t)]}{1 + W [F (t)]}

Տես նաև

Ծանոթագրություններ

Կաղապար:Ծանցանկ Կաղապար:Ծանցանկ

Արտաքին հղումներ

Միխաելիսի հաստատունի որոշում

↑ ^1,0 ^1,1 Introduction to Enzymes Կաղապար:Ref-en
↑ Henri, Victor (1903), Lois Générales de l’Action des Diastases. Paris: Hermann. Google books Կաղապար:Ref-en
↑ Վիկտոր Անրիի կենսագրություն Կաղապար:Ref-en
↑ ^4,0 ^4,1 Michaelis, L.; Menten, M.L. (1913). "Die Kinetik der Invertinwirkung". Biochem Z 49: 333–369
↑ Chen, W.W.; Neipel, M.; Sorger, P.K. (2010)Կաղապար:Ref-en
↑ ^6,0 ^6,1 Lehninger, A.L.; Nelson, D.L.; Cox, M.M. (2005). Lehninger principles of biochemistry. New York: W.H. Freeman
↑ ^7,0 ^7,1 Chakraborty, S. (23 Dec 2009). Microfluidics and Microfabrication (1 ed.). Springer.
↑ Chen, W.W.; Neipel, M.; Sorger, P.K. (2010). "Classic and contemporary approaches to modeling biochemical reactions". Genes Dev 24 (17): 1861–1875.
↑ Yu, R.C.; Rappaport, S.M. (1997). "A lung retention model based on Michaelis–Menten-like kinetics". Environ Health Perspect 105 (5): 496–503.
↑ Keating, K.A.; Quinn, J.F. (1998). "Estimating species richness: the Michaelis–Menten model revisited". Oikos 81 (2): 411–416.
↑ Jones, A.W. (2010). "Evidence-based survey of the elimination rates of ethanol from blood with applications in forensic casework". Forensic Sci Int 200 (1–3): 1–20.
↑ Abedon, S.T. (2009). "Kinetics of phage-mediated biocontrol of bacteria". Foodborne Pathog Dis 6 (7): 807–15.
↑ Mathews, C.K.; van Holde, K.E.; Ahern, K.G. (10 Dec 1999). Biochemistry (3 ed.). Prentice Hall
↑ Stroppolo, M.E.; Falconi, M.; Caccuri, A.M.; Desideri, A. (Sep 2001). "Superefficient enzymes". Cell Mol Life Sci 58 (10): 1451–60.
↑ ^15,0 ^15,1 ^15,2 Murray, J.D. (2002). Mathematical Biology: I. An Introduction (3 ed.). Springer.
↑ ^16,0 ^16,1 ^16,2 ^16,3 ^16,4 ^16,5 ^16,6 ^16,7 Keener, J.; Sneyd, J. (2008). Mathematical Physiology: I: Cellular Physiology (2 ed.). Springer
↑ A Note on the Kinetics of Enzyme Action Կաղապար:Ref-en
↑ Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences Կաղապար:Ref-en
↑ Grima, R.; Schnell, S. (Oct 2006). "A systematic investigation of the rate laws valid in intracellular environments". Biophys Chem 124 (1): 1–10.
↑ Schnell, S.; Turner, T.E. (2004). "Reaction kinetics in intracellular environments with macromolecular crowding: simulations and rate laws". Prog Biophys Mol Biol 85 (2–3): 235–60.
↑ ^21,0 ^21,1 Segel, L.A.; Slemrod, M. (1989). "The quasi-steady-state assumption: A case study in perturbation". Thermochim Acta 31 (3): 446–477.
↑ ^22,0 ^22,1 Leskovac, V. (2003). Comprehensive enzyme kinetics. New York
↑ Կաղապար:Cite journal Կաղապար:Ref-en
↑ Կաղապար:Cite journal Կաղապար:Ref-en
↑ Կաղապար:Cite journal Կաղապար:Ref-en
↑ Կաղապար:Cite journal Կաղապար:Ref-en

[Worthington-1] 1,0 ^1,1 Introduction to Enzymes Կաղապար:Ref-en

[2] Henri, Victor (1903), Lois Générales de l’Action des Diastases. Paris: Hermann. Google books Կաղապար:Ref-en

[3] Վիկտոր Անրիի կենսագրություն Կաղապար:Ref-en

[michaelis13-4] 4,0 ^4,1 Michaelis, L.; Menten, M.L. (1913). "Die Kinetik der Invertinwirkung". Biochem Z 49: 333–369

[5] Chen, W.W.; Neipel, M.; Sorger, P.K. (2010)Կաղապար:Ref-en

[nelson00-6] 6,0 ^6,1 Lehninger, A.L.; Nelson, D.L.; Cox, M.M. (2005). Lehninger principles of biochemistry. New York: W.H. Freeman

[chakraborty09-7] 7,0 ^7,1 Chakraborty, S. (23 Dec 2009). Microfluidics and Microfabrication (1 ed.). Springer.

[chen10-8] Chen, W.W.; Neipel, M.; Sorger, P.K. (2010). "Classic and contemporary approaches to modeling biochemical reactions". Genes Dev 24 (17): 1861–1875.

[yu97-9] Yu, R.C.; Rappaport, S.M. (1997). "A lung retention model based on Michaelis–Menten-like kinetics". Environ Health Perspect 105 (5): 496–503.

[keating98-10] Keating, K.A.; Quinn, J.F. (1998). "Estimating species richness: the Michaelis–Menten model revisited". Oikos 81 (2): 411–416.

[jones10-11] Jones, A.W. (2010). "Evidence-based survey of the elimination rates of ethanol from blood with applications in forensic casework". Forensic Sci Int 200 (1–3): 1–20.

[abedon09-12] Abedon, S.T. (2009). "Kinetics of phage-mediated biocontrol of bacteria". Foodborne Pathog Dis 6 (7): 807–15.

[mathews99-13] Mathews, C.K.; van Holde, K.E.; Ahern, K.G. (10 Dec 1999). Biochemistry (3 ed.). Prentice Hall

[stroppolo01-14] Stroppolo, M.E.; Falconi, M.; Caccuri, A.M.; Desideri, A. (Sep 2001). "Superefficient enzymes". Cell Mol Life Sci 58 (10): 1451–60.

[murray02-15] 15,0 ^15,1 ^15,2 Murray, J.D. (2002). Mathematical Biology: I. An Introduction (3 ed.). Springer.

[keener08-16] 16,0 ^16,1 ^16,2 ^16,3 ^16,4 ^16,5 ^16,6 ^16,7 Keener, J.; Sneyd, J. (2008). Mathematical Physiology: I: Cellular Physiology (2 ed.). Springer

[briggs25-17] A Note on the Kinetics of Enzyme Action Կաղապար:Ref-en

[zhou08-18] Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences Կաղապար:Ref-en

[grima07-19] Grima, R.; Schnell, S. (Oct 2006). "A systematic investigation of the rate laws valid in intracellular environments". Biophys Chem 124 (1): 1–10.

[schnell04-20] Schnell, S.; Turner, T.E. (2004). "Reaction kinetics in intracellular environments with macromolecular crowding: simulations and rate laws". Prog Biophys Mol Biol 85 (2–3): 235–60.

[segel89-21] 21,0 ^21,1 Segel, L.A.; Slemrod, M. (1989). "The quasi-steady-state assumption: A case study in perturbation". Thermochim Acta 31 (3): 446–477.

[leskovac03-22] 22,0 ^22,1 Leskovac, V. (2003). Comprehensive enzyme kinetics. New York

[23] Կաղապար:Cite journal Կաղապար:Ref-en

[24] Կաղապար:Cite journal Կաղապար:Ref-en

[25] Կաղապար:Cite journal Կաղապար:Ref-en

[26] Կաղապար:Cite journal Կաղապար:Ref-en

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

Միխաելիս-Մենթենի հավասարում

Բովանդակություն

Նախատիպ

Կիրառություն

Կինետիկական բնութագիր

Հավասարակշռային մոտավորություն

Քվազիստացիոնար մոտավորություն

Մոտավորություններ և սահմանափակումներ

Հաստատունների որոշում

Տես նաև

Ծանոթագրություններ

Արտաքին հղումներ

Նավարկման ցանկ

Միխաելիս-Մենթենի հավասարում

Նախատիպ

Կիրառություն

Կինետիկական բնութագիր

Հավասարակշռային մոտավորություն

Քվազիստացիոնար մոտավորություն

Մոտավորություններ և սահմանափակումներ

Հաստատունների որոշում

Տես նաև

Ծանոթագրություններ

Արտաքին հղումներ

Նավարկման ցանկ

Որոնում