Մաթեմատիկայի պատմությունը Հայաստանում

Մաթեմատիկայի պատմությունը Հայաստանում սկզբնավորվում է դեռևս Ուրարտական թագավորության ժամանակներից (մ. թ. ա. 9-7-րդ դարեր), երբ հայտնաբերվեցին հաշվարկման տասական և վաթսունական համակարգերը, և դրանք գրվում էին սեպագիր արձանագրությունների տեսքով։ Հայաստանի հին ժամանակվա թվաբանության և ուրարտական ժամանակաշրջանի թվաբանության մեջ անմիջական կապ գոյություն ուներ։ Ուրարտական ժամանակաշրջանի թվաբանությունը իր հետքն է թողել հին Հայաստանի թվաբանության վրա, որտեղ ապրել և աշխատել է Անանիա Շիրակացին։

V դարում՝ հայկական գրի ստեղծումից հետո, որպես թվանշաններ օգտագործվում էին հայկական տառերը։ Մաթեմատիկայի բնագավառում առաջին հայ գիտնականներից էր VII դարի ականավոր գիտնական Անանիա Շիրակացին։ Նա եղել է թվաբանության հայտնի դասագրքի հեղինակը։ 7-րդ դարի հայտնի մաթեմատիկներից էին նաև Լեո Մաթեմատիկոսը, Նիկողայոս Արտավազդը, Հովհաննես Իմաստասերը, Գրիգոր Մագիստրոսը։

XVII-XIX դարերում հայկական մի շարք շրջաններում բացվում են հայկական դպրոցներ, որտեղ ուսուցանվում էի մաթեմատիկա։ Այդ ժամանակաշրջանում բուռն կերպով հրատարակվում էին մաթեմատիկական գրքեր՝ հայերեն լեզվով։ Արդեն XVII-XIX դարերում կար ավելի քան 90 դասագիրք, որոնց հեղինակները հայ մաթեմատիկոսներն էին։

XX դարում Երևանում բացվում են Երևանի պետական համալսարանը (1921), Երևանի պոլիտեխնիկական համալսարանը (1931), Երևանի մանկավարժական համալսարանը (1922), ՀԽՍՀ Գիտությունների ակադեմիան (1943), որտեղ անցկացվում էին դասընթացներ ֆունկցիաներից, ֆունկցիաների հետազոտումից, ինտեգրալ և դիֆերենցիալ հավասարումներից և մաթեմատիկայի այլ բնագավառներից։

Հին դարեր և միջնադար

Ուրարտու

Ամենահին աղբյուրները մաթեմատիկայի հետ կապված, Հայաստանում հայտնաբերվել են Ուրարտական թագավորության ժամանակաշրջանում՝ սեպագիր արձանագրությունների տեսքով (մ. թ. ա. IX-VII դարեր)։ Նրանք վկայում են, որ այդ ժամանակ եղել է հաշվարկման տասական և վաթսունական համակարգերըԿաղապար:Sfn։ Տասական համակարգը արմատապես տարբերվում էր եգիպտականից և մոտ էր մեր նորագույն համակարգինԿաղապար:Sfn։ Սեպագիր արձանագրությունները ցույց են տալիս, որ մի քանի սիմվոլների օգնությամբ նրանք կարողացել են գրել բավականին մեծ ամբողջ և կոտորակային թվեր, և դրանց հետ կատարել են գումարման և հանման գործողություններԿաղապար:Sfn։ Ահա մի քանի օրինակներ, որոնք վերցված են Սարդուրի երկրորդի արձանագրություններից, որտեղ միավորները՝ , տասնավորները՝ , հարյուրավորները՝ և հազարավորները՝ Կաղապար:Sfn։

Ուրարտական սեպագիր արձանագրությունների օրինակ

23 — 8135 — 25000 — 6000 — 2500 — 12300 — 32100 —

Ուրարտացիները բարձր են գնահատել ասորա-բաբելական մշակույթը, վերցրել են նրանցից իրենց սեպագիր արձանագրությունները, ստեղծել են սեփական գիրը և գրականությունը, սեպագիր նշանների միջոցով գրառել են թվեր և գրել են բավականին մեծ թվերԿաղապար:Sfn։ Ուրարտական թագավորության և հին Հայաստանի թվաբանության մեջ գոյություն ունի անմիջական կապԿաղապար:Sfn։

Հայկական այբուբենի ստեղծումը

Հայերի մաթեմատիկական գիտելիքները, հատկապես V-VI դարերում, կարող էր ստանալ մեկ ընդհանուր գաղափար, մի կողմից ըստ փիլիսոփայական և պատմական աշխատանքների, որոնք ուսումնասիրում են որոշ խնդիրներ՝ մաթեմատիկայի և աստղագիտության հետ կապված, մյուս կողմից մշակույթի համար (բերդեր, ամրոցներ, պալատներ, եկեղեցիներ, կամուրջներ և ոռոգման համակարգ), որի համար պետք էին մաթեմատիկական գիտելիքների և ճիշտ հաշվարկներ, ինչպես նաև խթան էր հանդիսանում Հայաստանի մասնակցությանը միջազգային առևտրին։ 5-րդ դարում և VI դարի սկզբին հայերը մեկնում էին շարունակելու ուսումը Ալեքսանդրիայում, Հռոմում և Աթենքում։ Այս մասին վկայում են V դարի հայ պատմիչներըԿաղապար:Sfn։

Մինչև անգամ ժամանակակից գիտնականները, պատմաբանները չեն կարող գտնել զուտ մաթեմատիկական տեքստեր հայերի կողմից, ինչպես նաև 5-րդ դարում, երբ Մեսրոպ Մաշտոցը ստեղծեց հայոց գրերըԿաղապար:Sfn։ Հայկական գրերի ստեղծումից հետո բացվեցին հայկական դպրոցներԿաղապար:Sfn, որոնցում ուսուցանվում էր մաթեմատիկա։ Հայկական տառերը օգտագործվել են որպես թվեր (օրինակ. Գ-3, Խ-40, Չ-700, Ք-9000), ստորև ներկայացված է աղյուսակը։ Հայերի և հույների այբբենական համակարգի մեջ կան որոշ նմանություններ և տարբերություններ։ Հայերը ունեն 36 տառ, իսկ հույները՝ 27։ Ուրարտական համակարգը օգտագործվել է այբուբենին զուգահեռ, մինչև, վերջապես դուրս է եկել գործածությունից։ Սակայն ուրարտական շրջանի հետքերը անցել են նոր սերունդներինԿաղապար:Sfn։

Այբբենական տասնորդական համակարգԿաղապար:Sfn

	1	2	3	4	5	6	7	8	9
Միավորներ	Ա	Բ	Գ	Դ	Ե	Զ	Է	Ը	Թ
Տասնավորներ	Ժ	Ի	Լ	Խ	Ծ	Կ	Հ	Ձ	Ղ
Հարյուրավորներ	Ճ	Մ	Յ	Ն	Շ	Ո	Չ	Պ	Ջ
Հազարավորներ	Ռ	Ս	Վ	Տ	Ր	Ց	Ւ	Փ	Ք

Անանիա Շիրակացի

Անանիա Շիրակացու արձանը Մատենադարանի մուտքի մոտ՝ Երևանում

Անանիա Շիրակացու թվաբանության դասագրքի էջերից մեկը, 1283 թվական

Հայոց լեզվով պահպաված հին մաթեմատիկական աշխատանքնեի հեղինակը եղել է 7-րդ դարի պատմիչ, ուսուցիչ և բնական գիտությունների հիմնադիր Անանիա Շիրակացին։ Այն փաստը, որ 5-6-րդ դարերում կային հայերեն լեզվով աշխատություններ, վկայում է հենց ինքը՝ Շիրակացին։ Նա նշել է նաև, որ ոչ միայն ինքն է ներդրում ունեցել մաթեմատիկայի ասպարեզում, այլ նաև օգտվել է իր նախնիների աշխատանքներից. Կաղապար:Քաղվածք

Անանիա Շիրակացին մեծ ավանդ է ունեցել մաթեմատիկայի զարգացման գործում։ Նա ստեղծել է թվաբանության դասագիրքը, որը բաղկացած էր մի քանի մասերից. գումարման և հանման գործողությունների աղյուսակներից, բազմապատկման և բաժանման գործողությունների աղյուսակներից, $\frac{6000}{n}$ տեսքի թվերի աղյուսակներից, որտեղ $n$ ընդունում էր հայոց այբուբենի բոլոր տառերի թվային արժեքները, և կլորացվում էր մինչև ամենամոտ ամբողջ թիվը («Վեցհազարյակ»)։ Հայաստանում նույնպես օգտագործել են $\frac{5000}{n},\frac{4000}{n}$ տեսքի և այլ տեսքի թվերԿաղապար:Sfn։ Անանիա Շիրակացին կազմել է նաև հետաքրքրաշարժ խնդիրների գիրք, որը բաղկացած է եղել 24 խնդիրներից և խնդիրների հետ եղել են դրանց պատասխանները («Խրախճանականներ»)։ Գրեթե բոլոր խնդիրների մեջ Շիրակացին ամփոփում է հայ ժողովրդի կյանքը. կա՛մ խոսում էր հայոց պատմության, կա՛մ դիմում էի հայկական միջոցներիԿաղապար:Sfn։ Խնդիրները գծային էին, օրինակ դրանցից մեկը (№ 22) վերաբերվում էր թվաբանական պրոգրեսիայի բաժանմանը։

7-րդ դարից սկսած Բյուզանդական կայսրությունը, որը քրիստոնյա պետություն էր, լուրջ պայքար է սկսում հեթանոսական գիտությունների և դրանց ներկայացուցիչների դեմ։ Կապված այս իրադարձությունների հետ մաթեմատիկայի կարևորությունը Հայաստանում կտրուկ ընկնում է։ Այս մասին գրել է Անանիա Շիրակացին իր ինքնակենսագրության մեջԿաղապար:SfnԿաղապար:Sfn։

Պատմաբանները վկայում են այն մասին, որ Հայաստանում մ. թ. ա. 1-ին դարում կիրառել են երկարության չափման հետևյալ միավորները. ասպարեզ (օդում), որը հավասար է քայլի $107\frac{1}{7}$ մասին, ասպարեզ (հողի վրա), որը հավասար է քայլի $142\frac{6}{7}$ մասին և $150$ քայլ, աստիճան, որը ներառում է $500$ ասպարեզ։ Մղոնը եղել է մոտավորապես $7$ ասպարեզ, իսկ այլ կերպ՝ $1000$ քայլ, $1050$ քայլ, քայլը՝ $6$ ոտնաչափ, իսկ ոտնաչափը $16$ ձեռք։ VII դարում Հայաստանում երկու քաղաքների միջև հեռավորությունը չափում էին մղոններով, իսկ օրինակ մոլորակների և Երկրի միջև հեռավորությունները ասպարեզովԿաղապար:Sfn։ Երկարության չափման մասին բոլոր տեղեկությունները գրված են Անանիա Շիրակացու «Աշխարհացույց» աշխատության մեջԿաղապար:Sfn։

Մաթեմատիկան Հայաստանում VII դարից հետո

Գրիգոր Մագիստրոս

Հետագայում Շիրակացու ավանդույթները շարունակեց բյուզանդական մաթեմատիկոս, մեխանիկ՝ Լեո Մաթեմատիկոսը (790-869)։ Նա Կոստանդնուպոլսում զբաղվում էր մաթեմատիկայի դասախոսությամբ և 863 թվականին ստեղծեց և դարձավ Կոստանդնուպոլսի համալսարանի առաջին ռեկտորը։ Մաթեմատիկայում Լեոն համակարգում է տառերը, ինչպես թվաբանական սիմվոլներ՝ ակնկալելով հանրահաշվի առաջացմանը. նա պարզեցնում է Դիոֆանտի բարդ սիմվոլիկան և քայլ է անում հանրահաշվի հետագա զարգացման համարԿաղապար:SfnԿաղապար:Sfn։ XI դարի սկզբին և XII դարում մաթեմատիկայի բնագավառում մեծ ավանդ է ունեցել Հովհաննես Իմաստասերը, հայտնի ինչպես Յոհան Սարկավագը (1045/1055-1129)։ Իր մաթեմատիկական աշխատանքները ցույց են տալիս, որ հայկական միջնակարգ դպրոցներում սովորում էին ոչ միայն գործնական և տեսական թվաբանություն այլ նաև թվերի տեսություն։ Իր աշխատանքներից մեկում նա բացահայտում է բազմապատկման աղյուսակի հայկական տարբերակը։ Նրա «Բազմանկյուն թվերը» գիրքը հիմնված է Նիկոմախի «Թվաբանություն» գրքի վրաԿաղապար:Sfn։ Նա նույնպես շարունակել է հայերեն թարգմանել Ֆիլոն Ալեքսանդրացու, Արիստոտելի, Էվկլիդեսի, Դիոնիսիոս Արիոպագոսցու, Գրիգոր Նյուսացու գործերըԿաղապար:Sfn։ Հովհաննես Իմաստասերը եղել է «Բազմանկյուն թվեր» գրքի հեղինակը, որը որպես դասագիրք օգտագործել են 11-12-րդ դարերումԿաղապար:Sfn։

Մաթեմատիկան Հայաստանում բարձր մակարդակի է հասնում XI-XIII դարերում, երբ բացվում են միջնադարյան մի շարք համալսարաններ. Գլաձորի համալսարանը (հիմնադրվել է 1282 թվականին), Տաթևի համալսարանը (հիմնադրվել է 1373 թվականին), դպրոցներ Անիում, Հաղպատում և այլ ուսումնական հաստատություններ, այդ թվում Հայաստանի սահմաններից դուրսԿաղապար:Sfn։

Շիրակացու ավանդույթները XIII դարում շարունակել է նաև բյուզանդացի մաթեմատիկոս՝ ծագումով հայ, Նիկողայոս ԱրտավազդըԿաղապար:Sfn։ Նրանից պահպանվել է ընդամենը երկու նամակ հունարեն լեզվով։ Նրանցից մեկը խոսում է այն մասին, թե ինչպես կարող ենք ձեռքի մատերով ցույց տալ 1-ից մինչև 9999 թվերը, իսկ մյուսը՝ թե ինչպես քառակուսի արմատ հանենք թվիցԿաղապար:Sfn։

Հայկական դպրոցներում օգտագործվում էր հույն կլասիկների գործերը։ Հայ գիտնականները կատարում էին այդ գործերի թարգմանությունները. Էվկլիդեսի «Սկզբունքներ»-ը հայերեն են թարգմանել մի քանի հեղինակներ։ Պահպանված մի քանի մասեր թարգմանել են և՛ Անանիա Շիրակացին, և՛ Գրիգոր Մագիստրոսը (թարգմանվել է անմիջապես հունարենից՝ 1051 թվականին),Կաղապար:SfnԿաղապար:Sfn և այլք։ Համաձայն Գարեգին Պետրոսյանի, Էվկլիդեսի «Սկզբունքներ»-ի թարգմանության ամենահինը տարբերակը՝ արաբականից հետո, եղել է Գրիգոր Մագիստրոսի թարգմանությունը։ Էվկլիդեսի «Սկզբունքներ»-ի պահպանված մասերում հանդիպում են հայերեն թարգմանությամբ աքսիոմներ և դրույթներ, որոնք կազմում են «Սկզբունքներ»-ի հիմքըԿաղապար:SfnԿաղապար:Sfn։ 1959 թվականին հայտնաբերվել է «Սկզբունքներ»-ի ևս մեկ թարգմանություն, որը կատարել է Գրիգոր Կեսարացին XVII դարումԿաղապար:Sfn։

XVII-XIX դարեր։ Հայկական մաթեմատիկական գրականություն

XVII-XVIII դարերում մաթեմատիկա գիտության հարցերը անհանգստացնում էին պատմաբաններին և փիլիսոփաներին։ Իրենց հրապարակած փաստաթղթերը հիմնականում վերաբերվում էին թվաբանությանը և երկրաչափությանըԿաղապար:Sfn։ Այդ ժամանակաշրջանում ստեղծվեցին գրքեր մաթեմատիկայի և մաթեմատիկական կրթության համար։ Առաջին տպագրված գիրքը հայերեն լեզվով եղել է «Թվերի արվեստ»-ը, որը ունեցել է 147 էջ և տպագրվել է 1675 թվականին՝ Մարսելում։ Հեղինակը անունը անհայտ է։ Նա գրքում նշել է, որ գիրքը գրում է դիլերների համար, քանի որ նրանք անգրագետ են եղել մաթեմատիկայիցԿաղապար:Sfn։ Նա իր գրքի մեջ չի օգտագործել հանման, բաժանման, բազմապատկման, հավասարման նշանները, իսկ համապատասխան նշաններ գրքի մեջ օգտագործել է։ Հաջորդ աշխատության մեջ օգտագործել է ֆրանսիական, իտալական, պարսկական և այլ մաթեմատիկական տերմիններԿաղապար:Sfn։ Ավելի ուշ պարզվել է, որ «Թվերի արվեստ»-ը Քրիստոֆոր Կլավին թարգմանել է լատիներենԿաղապար:Sfn։ XVII դարում առանց հեղինակի անվան և ճշգրիտ ժամանակի, հրապարակվել է 120 էջանոց գիրք՝ դրանցից 109-ը թվաբանական աղյուսակներով. քառակուսի թվերի աղյուսակ՝ 1-100, բազմապատկման աղյուսակ՝ 1-100Կաղապար:Sfn։ 1781 թվականին Վենեցիայում հրատարակվել է Սուքիաս Աղամալյանցի «Թվաբանություն գիրքը», որը ունեցել է 511 էջԿաղապար:Sfn։ Գիրքը ներառում է նյութեր ոչ միայն հանման, գումարման, բազմապատկման, բաժանման մասին այլ նաև թվաբանական, երկրաչափական պրոգրեսիաների մասին և լոգարիթմի մասինԿաղապար:Sfn։ 1794 թվականին կրկին Վենեցիայում հրատարակվում է Սահակ Պրոնյանի «Երկրաչափություն» գիրքը, որի ծավալը կազմում է 423 էջԿաղապար:Sfn։ Գիրքը նվիրված է երկրաչափականթեորեմներին, աքսիոմներին և երկրաչափական տերմինների բացատրությանը (կոր, անկյուն, եռանկյուն, շրջանագիծ և այդպես շարունակ)Կաղապար:Sfn։ Սահակ Պրոնյանի մահից հետո՝ 1810 թվականին, Վենեցիայում հրատարակվում է նրա «Եռանկյունաչափություն» գիրքը։ Այս գրքի մեջ պատմության մեջ առաջին անգամ օգտագործվում է մաթեմատիկական նշաններԿաղապար:Sfn։ Գիրքը նվիրված է եռանկյունաչափությանը, եռանկյունների լուծմանը և ոլորտային երկրաչափությանը։

Էջեր հայերեն մաթեմատիկական գրքերից

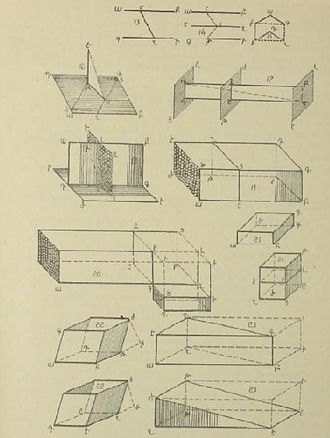
Հայերեն տպագրված առաջին գրքի՝ «Թվերի մշակույթ»-ի, առաջին էջը. 1675 թվական, Մարսել		17-րդ դարում Էվկլիդեսի «Սկզբունքներ»-ի հայերեն հրատարակության գծագրերը

XVII-XVIII դարերում հայերեն մաթեմատիկական գրականության մեջ օգտագործվում էին ռուսերեն տերմիններ։ 1744, 1753 և 1807 թվականներին Աստրախանի Հայաստանի ձեռագրերին նվիրված արվեստի կենտրոնում, պարունակվել են այնպիսի խնդիրներ, որոնցում օգտագործվել է «ռուբլի», «կոպեկ» և այսպիսի շատ ռուսական անվանումներԿաղապար:Sfn։ Ռուսական դպրոցները Աստրախանում, որոնք սովորեցնում են շատ առարկաներ, այդ թվում նաև երկրաչափություն, ավարտում են հայ բնակչության մի քանի ներկայացուցիչներ, իսկ մնացածը չեն կարողանում՝ կրթության համար գումար վճարել չկարողանալու պատճառովԿաղապար:Sfn։ 1810 թվականի դեկտեմբերի 12-ին Աստրախանում բացվում է Աղաբաբյան դպրոցը, որտեղ հայ բնակչության մեծ մասը հնարավորություն ունեցավ սովորելուԿաղապար:Sfn։ 1828 թվականին Արևելյան Հայաստանում, որը այդ ժամանակ Ռուսական կայսրության տիրապետության տակ էր, սկսվեցին բացվել կրթական հաստատություններԿաղապար:Sfn։ 1838 թվականի դեկտեմբերի 9-ին Կոստանդնուպոլսում բացվում է Սկյուտարի վարժարանըԿաղապար:Sfn, որտեղ ուսուցիչները հայեր են լինում՝ ստացած եվրոպական կրթություն։

Ղուկաս Տերտերյանցի մեծ աշխատանքները հրատարակվում են Վիեննայում։ 1843 թվականին միանգամից հրատարակվում է երկու գիրք՝ «Թվաբանություն» և «Տարրական երկրաչափություն»։ 1846 թվականին հրատարակվում է «Եռանկյունաչափություն և կոնաձև մարմիններ» գիրքը, որի ծավալը կազմում էր 134 էջԿաղապար:Sfn։ Գրքի երկրորդ մասը վերաբերվում էր անալիտիկ երկրաչափությանը։ Գրքի վերջում ներկայացված է 34 երկրաչափական գծագրություն։

XVII-XIX դարերում հայ հեղինակների կողմից ստեղծվեցին ավելի քան 90 հայկական գրքերԿաղապար:Sfn։

XX-XXI դարեր

XX դար

1921 թվականին Երևանում բացվում է հայկական համալսարանԿաղապար:Sfn։ Մաթեմատիկայի ուսուցումը սկսվեց համալսարանի տեխնիկական ֆակուլտետի և բնական գիտությունների ֆակուլտետի հիմնադրման ժամանակ, իսկ մաթեմատիկոսներ սկսվեցին պատրաստվել 1924 թվականից՝ ֆիզմաթ ֆակուլտետի հիմնադրումից հետոԿաղապար:Sfn։ 1921-1933 թվականներից համալսարանը պատրաստում էր մաթեմատիկայի ուսուցիչներ՝ ընդհանուր և միջնակարգ դպրոցներում դասավանդելու համարԿաղապար:Sfn։ Արդեն 1933 թվականին Երևանի պետական համալսարանը անցավ ուսուցման 5-ամյա պլանին, և սկսեցին պատրաստել մաթեմատիկոս-գիտնականներԿաղապար:Sfn։ 1959 թվականին ֆիզմաթ ֆակուլտետում ստեղծվում են մեխանիկա-մաթեմատիկական և ֆիզիկական ֆակուլտետները։ 1963 թվականին սկսում են պատրաստել գիտնականներ կիբեռնետիկայի ոլորտում, իսկ 1972 թվականին ստեղծվում է կիրառական մաթեմատիկայի և ինֆորմատիկայի ֆակուլտետը։

Մաթեմատիկայի անկախ գիտական և ստեղծագործական ոլորտը Խորհրդային Հայաստանում սկսվել է 1937-1941 թվականներին, երբ Երևանի պետական համալսարանի ֆիզմաթ ֆակուլտետի մի քանի ուսանողներ մեկնեցին ուսումը շարունակելու Մոսկվայում և Սանկտ-Պետերբուրգում՝ պաշտպանեցին թեզ և վերադարձան ԵրևանԿաղապար:Sfn։

1943 թվականին հիմնադրվում է ՀԽՍՀ գիտությունների ակադեմիան։ 1944 թվականին ՀԽՍՀ-ում ստեղծվում է մեխանիկայի և մաթեմատիկայի գրասենյակ։ Ավելի ուշ վարչությունը վերակազմավորում է մաթեմատիկայի և մեխանիկայի հայկական ազգային համալսարանը։ 1971 թվականին մաթեմատիկայի համալսարանը դարձավ անկախ կազմակերպություն։ 1956 թվականին ստեղծվեց մաթեմատիկական մեքենաների գիտահետազոտական համալսարանը։ 1957 թվականին ստեղծվում է Հայաստանի Խորհրդային Սոցիալիստական Հանրապետության համակարգչային կենտրոնը, որտեղ սկսեցին ուսումնասիրել կիբեռնետիկայի և համակարգչային տեխնիկայի խնդիրները, մաթեմատիկական ծրագրային ավտոմատացումը։ կիրառական մաթեմատիկայի, ինֆորմատիկայի և համակարգչային մեծ կենտրոն էր հանդիսանում նաև Հայաստանի պետական պոլիտեխնիկական համալսարանը։ 1961 թվականին Հայաստանի պետական պոլիտեխնիկական համալսարանը ստեղծում է համակարգչային համակարգերի և ինֆորմատիկայի ֆակուլտետ։ Համալսարանում կային նաև կիրառական մաթեմատիկայի, կիբեռնետիկայի և ֆիզիկայի ֆակուլտետներ։

Հայաստանում մաթեմատիկական դպրոցի հիմնադիրը եղել է Հայաստանի գիտությունների ազգային ակադեմիայի անդամ՝ Արտաշես Շահինյանը (1906-1978)Կաղապար:Sfn։ Արտաշես Շահինյանը եղել է առաջին հայ խորհրդային մաթեմատիկոսըԿաղապար:Sfn։ Լենինգրադյան համալսարանի ասպիրանտուրան ավարտելուց հետ նա 1937 թվականին վերադառնում է Երևան, միաժամանակ զբաղվում է և՛ գիտական աշխատանքով, և՛ աշխատում էԿաղապար:Sfn։ Մաթեմատիկայի հայկական դպրոցի ուսանողներից են եղել՝ Մխիթար Ջրբաշյանը, Սերգեյ Մերգելյանը, Ռաֆայել Ալեքսանդրյանը, Նագուշ Հարությունյանը, Գարեգին ՊետրոսյանըԿաղապար:Sfn, Վաչագան Սաղաթելյանը, Իշխան Խաչատրյանը, Գոհար Համբարձումյանը, Վանիկ Զաքարյանը, Նորայր Առաքելյանը և այլք։

Հայաստանի Գիտությունների ազգային ակադեմիայի շենքը	Երևանի պետական համալսարանի շենքը	Հայաստանի ազգային պոլիտեխնիկական համալսարանի շենքը

Մոտեցում տեսությանը

Հետազոտության հարցերին ամբողջովին սկսեցին պատասխանել 1930-ական թվականներին՝ Արտաշես ՇահինյանըԿաղապար:Sfn և ակտիվ կերպով շարունակեցին 1940-ական թվականներին՝ Հայաստանի ազգային ակադեմիայի անդամ Մխիթար Ջրբաշյանը (1918-1994) և Սերգեյ Մերգելյանը (1928—2008)Կաղապար:SfnԿաղապար:Sfn։ Ուսումնասիրվում են ֆունկցիաների իրար մերձենալու օրենքները, և այնպիսի հարցերի, որոնք վերաբերվում են ինտեգրալային և հավասարակշռված մատրիցներինԿաղապար:Sfn։ Այդ դեպքում ինտեգրալը ճշգրիտ ստացվել է որոշ լայն խմբերի տիրույթներում։ Դա եղել է ամբողջ թվային առանցքի վրա միակ լուծումըԿաղապար:Sfn։ 1940 թվականից հայկական մաթեմատիկական դպրոցներում սկսվում է կազմակերպվել ֆունկցիաների մասին դասերԿաղապար:Sfn։

Սերգեյ Մերգելյանին հաջողվել է ստանալ բազմանդամ՝ կոմպլեքս հարթության համարԿաղապար:Sfn։ Այս եղանակը հաջողությամբ կիրառվում է նաև ռացիոնալ ֆունկցիաների դեպքում, լավագույն դեպքում մի բազմանդամային մերձեցումովԿաղապար:Sfn։ Այս աշխատանքների համար Սերգեյ Մերգելյանը ստացել է Ստալինյան մրցանակ։

1950-ական թվականներին Մխիթար Ջրբաշյանը սկսել է հետազոտությունները բոլոր ֆունկցիաների միջինը, միատարրը և շոշափողը որոշելու համար, և այս աշխատանքները հաջողվել են միայն 1960-1970-ական թվականներինԿաղապար:Sfn։

Մոտավորությունների տեսություն

Կոմպլեքս տիրույթում բազմանդամների լրիվության հարցերի ուսումնասիրությունը Հայաստանում սկսվել է դեռևս 1930-ական թվականների վերջերին (Արտաշես Շահինյան) և բուռն զարգացում ապրել 1940-50-ական թվականներինին (Արտաշես Շահինյան, Մխիթար Ջրբաշյան, Սերգեյ Մերգելյան)։ Ուսումնասիրվել են բազմանդամներով մոտավորությունների հնարավորության, ինչպես նաև լավագույն մոտավորության հարցերը ինտեգրալային և կշռյալ-հավասարաչափ մատրիցների համար։ Ինտեգրալային մատրիցների համար ստացվել են լրիվության մի շարք ճշգրիտ հայտանիշներ՝ տիրույթների որոշ լայն դասերի համար։ Ստացվել է կշռյալ-հավասարաչափ բազմանդամային մոտավորության խնդրի լրիվ լուծումը իրական առանցքի համար։ Առաջադրվել ու լուծվել են իրական առանցքի վրա կշռյալ-լավագույն մոտավորությունների մի շարք ընդհանուր խնդիրներ (Մխիթար Ջրբաշյան)։ Ակադեմիկոս Մստիսլավ Կելդիշի (Մոսկվա) մեթոդի հետագա զարգացման ճանապարհով սպառիչ լուծում է ստացել կոմպլեքս հարթության վրա բազմանդամներով հավասարաչափ մոտարկման խնդիրը (Սերգեյ Մերգելյան)։ Այդ մեթոդը նա հաջողությամբ օգտագործել է նաև ռացիոնալ ֆունկցիաներով հավասարաչափ մոտավորության հնարավորության, ինչպես նաև լավագույն բազմանդամային մոտավորությունների հարցերում (Սերգոյ Մերգելյան, ԽՍՀՄ Պետական մրցանակ՝ 1952)։ 1950-ական թվականներին սկսվել են հետազոտություններն ամբողջ ֆունկցիաներով միջին, հավասարաչափ ու շոշափումային մոտավորությունների վերաբերյալ (Մխիթար Ջրբաշյան), որոնք 1960-70-ական թվականներիին ստացել են համակարգված բնույթ։ Վերջնական լուծում է տրվել տիրույթում անալիտիկ (մասնավորապես՝ ամբողջ) ֆունկցիաներով հավասարաչափ մոտավորության խնդրին։ Լիովին լուծվել է շոշափումային մոտավորության արագության նկարագրման խնդիրը։ Ստացվել են ամբողջ ֆունկցիաներով լավագույն մոտավորությունների վերաբերյալ մի շարք ընդհանուր ճշգրիտ լուծումներ (Նորայր Առաքելյան, ՀամԼԿԵՄ մրցանակ՝ 1970)։ Ամբողջ ֆունկցիաներով մոտավորությունների տեսության արդյունքներն ու մեթոդները հաջողությամբ կիրառվել են մի նոր բնագավառի՝ արժեքների բաշխման տեսության մեջ (Նորայր Առաքելյան և ուրիշներ)։ 1970-ական թվականներիից ծավալուն հետազոտություններ են կատարվել անալիտիկ ֆունկցիաների տարբեր համակարգերի լրիվության ու բազիսայնության վերաբերյալ (Մխիթար Ջրբաշյան և ուրիշներ)։ Արժեքավոր արդյունքներ են ստացվել դասավանդումը անալիտիկ շարունակության հարցերի և կոմպլեքս մոտավորությունների տեսության փոխադարձ կապի վերաբերյալ (Նորայր Առաքելյան և ուրիշներ)։

Ֆունկցիաների ընդհանուր տեսություն

Այս բնագավառում լուրջ հետազոտություններն սկսվել են 1945 թվականից, երբ սկսվել է շրջանում անսահմանափակ տեսքի մերոմորֆ ֆունկցիաների ֆակտորացման տեսության կառուցումը (Մխիթար Ջրբաշյան)։ Այդ աշխատանքները և ստացված արդյունքներն էական առաջընթաց էին 1924 թվականին Ռոլֆ Նևանլինայի ստացած դասական արդյունքից հետո և լուրջ ազդեցություն ունեցան Հայաստանում անալիտիկ և մերոմորֆ ֆունկցիաների տեսության բնագավառում կատարվող հետազոտությունների վրա։ Հետազոտությունների մյուս խոշոր շարքն ընդգրկում է կոմպլեքս տիրույթում հարմոնիկ անալիզի և դրա հետ սերտորեն առնչվող ֆունկցիաների ինտեգրալ ձևափոխությունների ու ներկայացումների տեսության հարցերը (1950-60-ական թվականներ)։ Ստացված արդյունքները ներկայացված են Մխիթար Ջրբաշյանի «Ինտեգրալ ձևափոխություններ և ֆունկցիաների ներկայացումներ կոմպլեքս տիրույթում» (ուսումնական, 1966) մենագրության մեջ։ Մխիթար Ջրբաշյանը կառուցել է Ֆուրիեի-Պլանշերելի տիպի ձևափոխությունների կատարյալ տեսությունը՝ մի կետից ելնող ճառագայթների կամայական համակարգի համար, նոր հիմնարար արդյունքներ ստացել ամբողջ ու անալիտիկ ֆունկցիաների ներկայացման հարցերում և ընդլայնել ու զարգացրել Վիների-Պելլիի՝ այս բնագավառում հայտնի դասական թեորեմները։ Մխիթար Ջրբաշյանը և նրա աշակերտները զարգացրել են կոմպլեքս տիրույթում դիսկրետ հարմոնիկ անալիզի տեսությունը. պարզվել է, որ այն սերտորեն առնչվում է նաև կոտորակային կարգի դիֆերենցիալ օպերատորների համար էապես նոր տիպի եզրային խնդիրների հետ։ 1963 թվականին վերսկսվել են հետազոտությունները մերոմորֆ ֆունկցիաների տեսության բնագավառում, սահմանվել են a պատկանում է (-1, + ∞) ֆունկցիաների հետ առնչվող մերոմորֆ ֆունկցիաների էապես նոր դասեր, որոնք ի վիճակի են ընդգրկելու շրջանում մերոմորֆ կամայական ֆունկցիաները, և զարգացվել է նրանց պարամետր. ներկայացման տեսությունը (Մխիթար Ջրբաշյան)։ Ուսումնասիրվել են այդ դասերի նուրբ եզրային հատկությունները (Մխիթար Ջրբաշյան, Վանիկ Զաքարյան)։ Շրջանում անալիտիկ ֆունկցիաների ֆակտորացման և այդպիսի ֆունկցիաների հանրահաշիվներում փակ իդեալների նկարագրությանն են նվիրված Ֆ. Շամոյանի աշխատանքները։ Մասնավորապես, Մխիթար Ջրբաշյանի ֆակտորացման թեորեմների և Н (α) դասերի ինտեգրալ ներկայացումների հիման վրա ստացվել են շրջանում վերջավոր կարգի մաժորանտ ունեցող անալիտիկ ֆունկցիաների պարամետր, ներկայացումները։ Ամբողջ և մերոմորֆ ֆունկցիաների դեֆեկտային արժեքների հարցերով զբաղվել են Նորայր Առաքելյանը և ուրիշներ։ Առաջին անգամ օգտագործելով մոտավորությունների տեսության մեթոդներն ու արդյունքները՝ Նորայր Առաքելյանը հերքել է Ռոլֆ Նևանլիևայի հայտնի վարկածը՝ վերջավոր կարգի ամբողջ ֆունկցիաների դեֆեկտային արժեքների մասին։ Մերոմորֆ ֆունկցիաների երկրաչափական տեսության և արժեքների բաշխման տեսության մեջ նոր էական արդյունքներ է ստացել Գրիգոր Բարսեղյանը՝ զարգացնելով Նևանլինայի-Լ. Ալֆորսի դասական տեսության որոշ մոտեցումներ։ Անալիտիկ ֆունկցիաների տեսության մեջ կատարվող հետազոտություններում նկատելի տեղ են գրավում միակության, ներառյալ նաև քվազիանալիտիկության հարցերը։ Զարգացնելով Է. Լինդելյոֆի հայտնի արդյունքները՝ Արտաշես Շահինյանը շրջանում անալիտիկ ֆունկցիաների համար ստացել է միակության «ներքին» ինտեգրալ հայտանիշներ, որոնք տարածել է շրջանում մերոմորֆ ֆունկցիաների վրա։ Այդ արդյունքների մի մասը Վանիկ Զաքարյանը տարածել է Մխիթար Ջրբաշյանի դասերի վրա։ Քվազիանալիտիկ դասերի ֆունկցիաների ներկայացման խնդիրն սկզբունքորեն լուծում էր ստացել Կառլեմանի և Բանգի աշխատանքներում։ Այդ խնդրին մեկ այլ լուծում է տվել Հայկ Բադալյանը՝ նույն ֆունկցիաները ներկայացնելով հատուկ շարքերի տեսքով։ Մխիթար Ջրբաշյանը, հիմնվելով կոմպլեքս տիրույթում հարմոնիկ անալիզի իր տեսության վրա, էապես ընդլայնել է Դանժուայի-Կառլեմանի դասական քվազիանալիտիկության գաղափարը՝ կառուցելով а-քվազիանալիտիկ դասերի տեսությունը։ Հետազոտություններ են կատարվել նաև բազմաչափ կոմպլեքս անալիզի, ինչպես նաև անալիտիկ ֆունկցիաների հանրահաշիվների բնագավառներում։

Իրական փոփոխականի ֆունկցիաների տեսություն

Ալեքսանդր Թալալյան

Հետազոտությունները կատարվել են 1950-ական թվականներիի կեսերից, որոնք սկզբնական շրջանում հիմնականում վերաբերում էին չափելի ֆունկցիաներն օրթոգոնալ (մասնավորապես՝ եռանկյունաչափական) շարքերով ներկայացման և այդ շարքերի միակության հարցերին։ Ալեքսանդր Թալալյանն ապացուցել է ընդհանուր բնույթի թեորեմներ, որոնց համաձայն՝ լրիվ օրթոգոնալ համակարգերի շարքերով կարող են ներկայացվել բոլոր չափելի ֆունկցիաները, և որ այդ շարքերը կարող են ունենալ նաև ցանկացած սահմանային ֆունկցիաների բազմություն։ 1965 թվականից նրա ղեկավարությամբ կատարվել են ընդհանուր օրթոգոնալ համակարգերի և բազիսների, ինչպես նաև որոշակի օրթոգոնալ համակարգերի (Ոտլշի, Հաարի և այլ եռանկյունաչափական համակարգեր) համակարգված հետազոտություններ։ Կարևոր արդյունքներ են ստացվել տարբեր իմաստներով ունիվերսալ օրթոգոնալ շարքերի գոյության վերաբերյալ։ Լուծվել են օրթոգոնալ շարքերի՝ դրական չափի բազմությունների վրա անվերջությանը զուգամիտելու հիմնախնդրին վերաբերող մի շարք խնդիրներ, որոնք որոշակի առաջընթաց են Լուզինի առաջադրած համապատասխան խնդրի լուծման ուղղությամբ։ Լուծվել է ինտեգրելի ֆունկցիաներին զուգամիտող Ոտլշի շարքերի գործակիցների վերականգնման խնդիրը, և ապացուցվել են Կանտորի ու Վալլե-Պուսսենի տիպի այնպիսի միակության թեորեմներ Հաարի և Ոտլշի համակարգերի համար, որոնց հանգունակները եռանկյունաչափական համակարգի դեպքում ճիշտ չեն կամ մինչ այդ հայտնի չէին։ Ապացուցվել են ընդհանուր բնույթի թեորեմներ, որոնց համաձայն՝ չափելի ֆունկցիաների համակարգերի լրիվության որոշ հատկություններ պահպանվում են նաև այդ համակարգերից վերջավոր թվով ֆունկցիաներ հեռացնելուց հետո։ Կարևոր արդյունքներ են ստացվել ոչ լրիվ մինիմալ համակարգերի մուլտիպլիկացիոն լրացման միջոցով բազիսներ ստանալու հարցում։ Տրվել են նաև օրթոգոնալ համակարգերի որոշ հատկությունների և այդ համակարգերով վերլուծությունների զուգամիտության կապի վերաբերյալ մի քանի կարևոր խնդիրների լուծումները։ Ստացվել են կարևոր թեորեմներ հավանական տարածություններում չափելի ֆունկցիաների մարտինգալներով ներկայացման, այդ մարտինգալների կառուցվածքի և նրանց միակության վերաբերյալ։

Ֆունկցիոնալ անալիզ

Հետազոտություններն սկսվել են 1950-ական թվականներին ԵՊՀ-ում և ՀԽՍՀ գիտությունների ակադեմիայի մաթեմատիկայի և մեխանիկայի սեկտորում, ուսումնասիրվել են նոր տիպի եզրային խնդիրները հիլբերտյան տարածության մեջ Կոշիի օպերատորային խնդրին հանգեցնելու հարցերը (Ռաֆայել Ալեքսանդրյան)։ Պտտվող հեղուկի որակ, տեսության մաթեմատիկական հետազոտություններին նվիրված աշխատանքների շարքի համար Ռաֆայել Ալեքսանդրյանը 1986 թվականին արժանացել է ԽՍՀՄ Պետական մրցանակի։ Հետագայում մի շարք մաթեմատիկոսների աշխատանքներով էապես ընդլայնվել է հետազոտությունների թեմատիկան ինչպես ֆունկցիոնալ անալիզի, այնպես էլ դիֆերենցիալ և ինտեգրալ հավասարումների բնագավառներում։ Հետազոտությունների հիմնական ուղղություններն են օպերատորների տեսությունը, օպերատորային հավասարումները, ինքնահամալուծ օպերատորային հավասարումները և դրանց սպեկտրային տեսությունը։ Կամայական ինքնահամալուծ օպերատորի ռեզոլվենտի տերմիններով ներմուծվել է սպեկտրի կորիզի գաղափարը, մշակվել է սեփական ֆունկցիոնալների լրիվ համակարգի կառուցման ունիվերսալ եղանակ, և ըստ այդ ֆունկցիոնալների՝ սպեկտրային վերլուծության վերաբերյալ թեորեմներ։ Ապացուցվել են նոր տիպի առնչություններ, որոնցից բխում են սպեկտրի որակ, բնույթը բնորոշող հայտանիշներ (Ռաֆայել Ալեքսանդրյան, Ռաֆայել Մկրտչյան)։ Բանախյան հանրահաշիվների տեսության մեջ ապացուցվել են թեորեմներ, որոնք զարգացնում են Հոֆմանի արդյունքները Սթոուն-Վայերշտրասի տիպի թեորեմների ընդհանրացման ուղղությամբ, ինչպես նաև Վեռների թեորեմների դիսկ-հանրահաշիվների մաքսիմալության և ընդհանրացրած անալիտիկ ֆունկցիաների հանրահաշիվների վերաբերյալ։ Հետազոտվել են որոշ դասերի բագմանդամային օպերատորային փնջի սպեկտրային հատկությունները, առաջարկվել է նրանց սեփական ֆունկցիոնալների կառուցման եղանակ։ Բացահայտվել են Շրեդինգերի հավասարումն ընդգրկող որոշ դասերի ոչ ստացիոնար օպերատորային հավասարումների լուծումների ասիմպտոտիկ համարյա պարբերականության պայմանները։

Դիֆերենցիալ և ինտեգրալ հավասարումներ

Մի քանի դիֆերենցիալ հավասարումների գրաֆիկների օրնակներ

Այս ասպարեզում 1930-ական թվականներին ստացվել են որոշ արդյունքներ պարաբոլական հավասարումների վերաբերյալ։ Համակարգված հետազոտություններ սկսվել են 1948 թվականիցից՝ Ռաֆայել Ալեքսանդրյանի աշխատանքներով, հիմն, ուղղություններն էին՝ էլիպսային, հիպոէլիպսային, հիպերբոլական ու թույլ հիպերբոլական և ինտեգրալ (այդ թվում՝ սինգուլյար ինտեգրալ) հավասարումները։ Հետազոտվել են նոր բնույթի եզրային խնդիրներ՝ որոշ ոչ դասական դիֆերենցիալ հավասարումների համակարգերի համար, Դիրիխլեի խնդիրը՝ լարի տատանման հավասարման համար, ներմուծվել է ընդհանրացված սեփական ֆունկցիայի հասկացությունը։ Մխիթար Ջրբաշյանը և Հանրի Ներսիսյանն առաջինն են դիտարկել նոր բնույթի եզրային խնդիրներ և սպեկտրային վերլուծություններ՝ կոտորակային կարգի դիֆերենցիալ օպերատորներին առնչվող։ Ուսումնասիրվել են Շտուրմի-Լիուվիլի խնդրի սպեկտրային վերլուծությունները, և ստացված արդյունքները տարածվել են Դիրակի միաչափ համակարգերի վրա (Իշխան Սարգսյան)։ Արդյունքները շարադրված են Բորիս Լևիտանի և Իշխան Սարգսյանի «Սպեկտրային տեսության ներածություն։ Ինքնահամալուծ սովորական դիֆերենցիալ օպերատորներ» (ուսումնական, 1970) մենագրությունում։ Ուսումնասիրվել են Շտուրմի-Լիուվիլի հակադարձ խնդիրը, ինչպես նաև բարձր կարգի հավասարումների դեպքում ցրման տեսության հակադարձ խնդիրը։ Հանրի Ներսիսյանն ուշացող արգումենտով հավասարման եզրային խնդրի համար ստացել է, ըստ սեփական ֆունկցիաների վերլուծության, թեորեմներ, մշակել է թույլ (ոչ խիստ) հիպերբոլական հավասարումների համար որոշ խնդիրների ուսումնասիրության եղանակ, ներմուծել և օգտագործել է Վոլտերայի ինտեգրալ հավասարման ընդհանուր հասկացությունը, ինչպես նաև առաջարկել ինտեգրալ օպերատորների շրջման մի եղանակ, երբ կորիզը բավարարում է մասնակի ածանցյալներով դիֆերենցիալ հավասարմանը։ Ոաումնասիրվել են որոշ ոչ ինքնահամալուծ դիֆերենցիալ օպերատորների սպեկտրի վարքը և գրգռումները։ Նազարեթ Թովմասյանը և ուրիշներ հետազոտել են Դիրիխլեի և Նեյմանի խնդիրները խզվող եզրային տվյալների դեպքում, ստացել մի շարք արդյունքներ ընդհանուր էլիպսային համակարգերի վերաբերյալ։ Հետազոտվել են նաև սովորական դիֆերենցիալ հավասարումներ՝ ընդհանրացված ֆունկցիաների դասում, ստացվել մի շարք արդյունքներ սինգուլյար ինտեգրալ հավասարումների վերաբերյալ (Նազարեթ Թովմասյան)։ Ուսումնասիրվել են Վիների-Հոպֆի ինտեգրալ հավասարումները եզակի դեպքում (Նազարեթ Թովմասյան, Նորայր Ենգիբարյան)։ Հետազոտվել են նաև ճառագայթման տեղափոխության տեսության ինտեգրալ և ինտեգրադիֆերենցիալ հավասարումները (Նորայր Ենգիբարյան)։ Հայկ Ղազարյանն ուսումնասիրել է ընդհանուր դիֆերենցիալ օպերատորներին համապատասխանող բազմանդամների վարքը և դրանով իսկ բացահայտել հիպոէլիպսականության պայմանը ոչ ռեգուլյար օպերատորների որոշ դասի համար, ինչպես նաև ստացել լուծումների որոշ գնահատականներ։

Երկրաչափություն, տոպոլոգիա, հանրահաշիվ

Երկրաչափության բնագավառում հետազոտություններն սկսվել են 1940-ական թվականներին ԵՊՀ-ում. ուսումնասիրվել են ուղղաձիգ կոնգրուենցիաների աֆինային տեսության հարցեր։ Հետագայում ուսումնասիրություններն ընդլայնվել են, աշխատանքներ են կատարվել բազմաչափ հարթությունների լոկալ-դիֆերենցիալ երկրաչափության, դասական համասեռ տարածություններում ենթաբազմաձևությունների երկակի նորմալացման և ենթաբազմաձևությունների լոկալ կառուցման, դիֆերենցելի շերտավորման վրա աֆինային կապերի ու տենզորական դաշտերի պրոյեկտման տեսության և այլ հարցերի վերաբերյալ։

Տոպոլոգիայի բնագավառում աշատանքներն սկսվել են 1970-ական թվականների սկգբներին։ Ներմուծվել են հիլբերտյան տարածության ենթաբազմությունների անվերջ չափանի նմանատեղային խմբերը, և վերջավոր դեֆեկտով սֆերայի համար հաշվվել կոմպակտ տիպի այդ խմբերը։ Ստացվել է կամայական հաուսդորֆյան տարածության բոլոր H-փակ (ինչպես նաև բոլոր հաուսդորֆյան) ընդլայնումների կառուցման՝ վաղուց դրված խնդրի լուծումը։ 1980-ական թվականներին Սթոուն-Վայերշտրասի մոտարկման դասական թեորեմն ընդհանրացվել է կամայական տոպոլոգիական տարածության համար (Ս. Հովսեփյան)։

Հանրահաշվի բնագավառում առաջին աշխատանքը կատարվել է 1950-ական թվականներին՝ մասնակի տեղադրությունների վերջավոր համակարգերի հետազոտման վերաբերյալ (Վ. Հովհաննիսյան)։ 1970-ական թվականներից աշխատանքներ են կատարվում քառակուսի մատրիցների ներկայացման, Լիի իրական ոչ կոմպակտ պարզ խմբերի վերլուծման, ունիվերսալ և երկրորդ աստիճանի հանրահաշիվներում երկրորդ աստիճանի նույնությունների հետազոտման, երկրորդ աստիճանի զուգորդ, նույնությունների դասակարգման, Պրիմի բազմաձևությունների՝ հիպերէլիպսային կորի երկու կետերում ճյուղավորման դեպքում ուսումնասիրման և այլ հարցերի վերաբերյալ։

Հավանականություններ տեսություն և մաթեմատիկական վիճակագրություն

Վիկտոր Համբարձումյան

Հետազոտություններն սկսվել են հետպատերազմյան տարիներին։ Ստացվել են մի շարք արդյունքներ պատահական շարժընթացների տեսության (Գոհար Համբարձումյան), իսկ ավելի ուշ՝ χ² հայտանիշի վերաբերյալ (Ս. Թումանյան)։ Ռուբեն Համբարձումյանի աշխատանքներով ստեղծվել է նոր ուղղություն՝ կոմբինատորային ինտեգրալ երկրաչափությունը, որը կարևոր կիրառություններ է ստացել ստոխաստիկ երկրաչափության խնդիրների հետազոտություններում, մասնավորապես լուծվել են երկրաչափական պատահական շարժընթացների տարածաբանությանը (ստերեոլոգիա, շերտագրություն) վերաբերող խնդիրներ։ Ստացված արդյունքները շարադրված են Ռուբեն Համբարձումյանի մենագրություններում։ Լուծվել են նաև զանգվածային սպասարկման տեսության խնդիրներ (Էդուարդ Դանիելյան), որոշ արդյունքներ են ստացվել ստոխաստիկ դիֆերենցիալ հավասարումների, վիճակագրական ֆիզիկայի, ինֆորմացիաների տեսության, պատահական շարժընթացների տեսության ասպարեզներում։

Մաթեմատիկական ֆիզիկա

Սկզբնավորվել է 1960-ական թվականներին՝ Վիկտոր Համբարձումյանի դասական աշխատանքներով, որոնցում առանձնահատուկ տեղ են գրավում ինվարիանտության սկզբունքը և Շտուրմի-Լիուվիլի հակադարձ խնդրի ձևակերպումն ու լուծումը։ Հետագայում մաթեմատիկական ֆիզիկական հետազոտությունները զարգացել են Նորայր Ենգիբարյանի աշխատանքներում։ մաթեմատիկական ֆիզիկայի դիֆերենցիալ, ինտեգրալ, ինտեգրալ-դիֆերենցիալ ու հանրահաշվական հավասարումների հետազոտման ու լուծան բնագավառում՝ ներառյալ փաթեթի տիպի հավասարումների լայն դասերը, մշակվել են մի շարք նոր մեթոդներ, որոնք կիրառվել են ճառագայթման տեղափոխման տեսության գծային և ոչ գծային ուղիղ և հակադարձ խնդիրներում, ֆիզիկական կինետիկայի, կիսամարկոփան շարժընթացների բնագավառներում։ Ստեղծվել է գծային օպերատորների ֆակտորացման ոչ գծային հավասարումների տեսությունը՝ ներառյալ ոչ շրջելի օպերատորների ֆակտոիացումն ու Միլնի ընդհանրացված հիմնախնդրի լուծումը։ Ստեղծվել է Համբարձումյանի ընդհանրացված հավասարումների տեսությունը։ Զարգացվել են կրիտիկական դեպքում անշարժ կետի նոր սկզբունքներ։ Դրվել են ըստ չափի ածանցյալ պարունակող դիֆերենցիալ հավասարումների տեսության հիմքերը։ Ապացուցվել է Համմերշտեյնի և Ուրիսոնի տիպի ոչ կոմպակտ օպերատորներով հավասարումների որոշ դասերի լուծելիությունը կրիտիկական դեպքում (Նորայր Ենգիբարյան, Լ. Արաբաջյան, Ա. Խաչատրյան, Մ. Մուրադյան, Խ. Խաչատրյան, Ա. Բարսեղյան, Հ. Հարությունյան)։

Գրականություն

• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն գիրք
• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն գիրք
• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն գիրք
• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն գիրք
• Կաղապար:Ռուսերեն գիրք
• Կաղապար:Ռուսերեն գիրք
• Կաղապար:Ռուսերեն գիրք
• Կաղապար:Ռուսերեն գիրք
• Կաղապար:Ռուսերեն հոդված
• Կաղապար:Ռուսերեն գիրք
• Կաղապար:Ռուսերեն գիրք